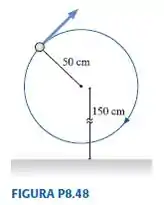
Uma bola de é presa à extremidade de um barbante de de comprimento e girada em um círculo vertical. O centro do círculo, como mostra a FIGURA , encontra-se acima do piso. A bola é girada com a mínima velocidade necessária para que atinja o topo sem que o barbante fique frouxo. Se a pessoa solta o barbante em um instante no qual a bola esteja no topo do loop, a que distância horizontal à direita a bola atingirá o solo?

Um instante antes de a lâmina cortar o barbante, temos a força tensora e a força gravitacional pra baixo. E a força resultante dessas duas forças é a força centrípeta:

E essa velocidade será a velocidade horizontal que a bola vai ter.

Mas o barbante é cortado, então temos que .

Os dados são:

Então é só resolver pra e substituir os valores, saca só:

Agora vamos achar o tempo. Da equação de queda livre temos:

A velocidade inicial vertical é zero, pois a bola é lançada horizontalmente. E a posição final é zero, pois queremos o tempo para que ela chegue ao chão. A posição inicial é , então agora é só substituir:

Por fim, com a velocidade e o tempo, podemos achar o alcance. O tempo em que a bola desce é o mesmo que ela se desloca horizontalmente, por isso usamos o mesmo tempo =)

Lembrando que na horizontal não temos aceleração, então o alcance é determinado por mru:

Beleza?

Espero ter ajudado!

Vamos pra próxima?