Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 10.Problemas - Ex. 1
Demonstre que duas adiabáticas nunca podem se cortar. Sugestão: Supondo que isto fosse possível, complete um ciclo com uma isoterma e mostre que a lei da termodinâmica seria violada se um tal ciclo existisse.
Passo 1
Vamos começar desenhando duas curvas adiabáticas se cortando em um diagrama , e completando o ciclo com uma isoterma:
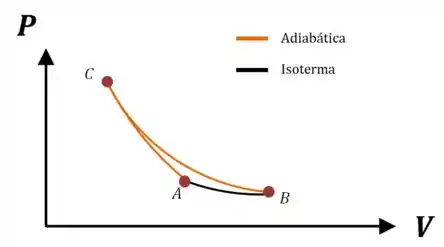
Agora queremos mostrar que isso viola a segunda lei da termodinâmica.
Passo 2
No processo ilustrado no gráfico, só há trocas de calor no trecho , quando o gás absorve calor para realizar trabalho.
Como está ao longo de uma isoterma, temos:
Então, pela primeira lei da termodinâmica:
Ou seja, estamos realizando que simplesmente remove calor e produz uma quantidade equivalente de trabalho, sem nenhum outro efeito.
Isso é proibido pela segunda lei da termodinâmica, e portanto aquele ciclo é impossível.
Passo 3
Para garantir que não vai sobrar nenhuma dúvida: o que mudaria se as adiabáticas não se interceptassem?
Se tivéssemos uma segunda isoterma na parte de cima do ciclo, o diagrama ficaria da seguinte forma:
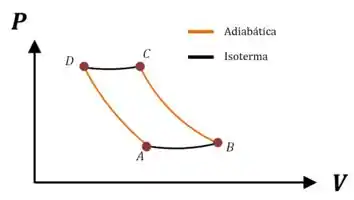
Nesse caso, além, de remover calor para produzir o trabalho no trecho , teríamos uma variação de entropia no trecho CD.
Essa variação não acontece nos trechos adiabáticos porque .
Resposta
Demonstração.