Um mol de gás ideal, com , está ocntido num recipiente, inicialmente a e . O gás é, sucessivamente: (i) comprimido isobaricamente até do volume inicial ; (ii) aquecido, a volume constante, até voltar à temperatura inicial; (iii) expandido a pressão constante até voltar ao volume inicial; (iv) resfriado, a volume constante, até voltar à pressão inicial. (a) Desenho o diagrama associado; (b) Calcule o trabalho total realizado pelo gás; (c) Calcule o calor total fornecido ao gás nas etapas (i) e (ii); (d) Calcule as temperaturas máxima e mínima atingidas; (e) Calcule a variação de energia interna no processo (i)+(ii).
Passo 1
(a) Podemos desenhar o diagrama da seguinte forma:
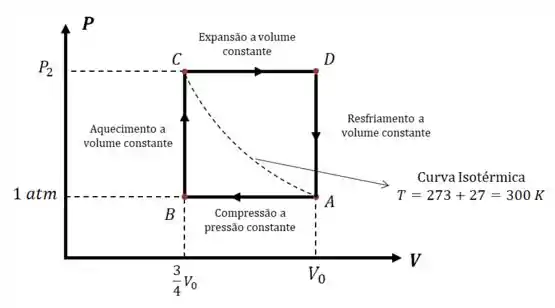
Aqui você só precisa seguir as instruções do enunciado, lembrando da relação:
O que significa que tanto a pressão quanto o volume são diretamente proporcionais à temperatura.
Vamos tentar encontrar os valores de e .
Passo 2
Podemos começar usando a lei dos gases ideais sobre o ponto :
A temperatura está em kelvin, a pressão em e o volume em litros:
E agora podemos comprar os pontos e para encontrar a pressão em :
As temperaturas são iguais nos dois pontos:
E a razão entre os dois volumes é :
Agora podemos completar o gráfico:
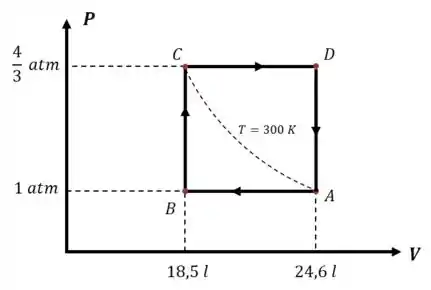
Passo 3
(b) Agora podemos calcular o trabalho realizado ao longo de um ciclo completo.
Nos trechos e o trabalho é nulo, já que o volume permanece constante. Então só precisamos considerar os trechos e :
Nos dois casos a pressão se mantém constante. No trecho :
Onde convertemos as unidades lembrando que , e .
E no trecho :
Então:
Passo 4
(c) Agora queremos calcular a quantidade de calor fornecido ao gás nas etapas (i) e (ii) (ou seja, o trecho ).
Nesse trecho, os pontos inicial e final estão à mesma temperatura, isso quer dizer que a variação de energia interna entre eles é nula:
Então, pela primeira lei da termodinâmica:
Ou seja, o calor fornecido ao gás é igual ao trabalho realizado por ele. Mas nós já calculamos esse valor no passo anterior:
E o sinal negativo indica que o calor é rejeitado pelo gás.
Passo 5
(d) Agora podemos calcular as temperaturas máxima e mínima atingidas pelo gás.
A temperatura mínima ocorre no ponto , e podemos calculá-la pela lei dos gases ideais:
E a temperatura máxima ocorre no ponto :
Passo 6
(e) O processo (i)+(ii) nos leva do ponto até o ponto .
Esses dois pontos estão sobre a mesma curva isotérmica. Ou seja, a temperatura é a mesma nos dois pontos, portanto a variação de energia interna é nula:
Resposta
(a) Ver desenho.
(b).
(c) O gás perde de calor.
(d) A temperatura máxima é e a mínima é .
(e) A variação de energia interna é nula nesse trecho.