Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 20.Problemas Adicionais - Ex. 51

( N 2 ) sofre um aumento de temperatura a volume constante, a distribuição de velocidades das moléculas se altera, ou seja, a função distribuição de probabilidade P ( v ) da velocidade das moléculas se torna mais larga, como mostra a figura abaixo.

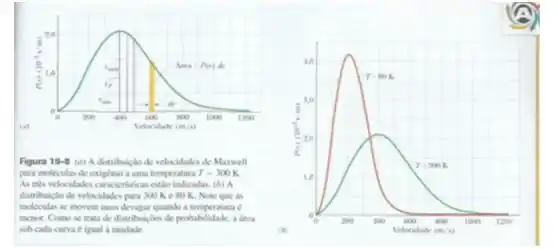
Uma forma de descrever esse alargamento de P ( v ) é medir a diferença Δ v entre a velocidade mais provável v p e a velocidade média quadrática v r m s . Quando P ( v ) se estende para velocidades maiores, Δ v aumenta. Suponha que o gás é ideal e que as moléculas de N 2 giram, mas não oscilam. Para 1,5 m o l de N 2 , uma temperatura inicial de 250 K e uma temperatura final de 500 K , qual é

a a diferença inicial Δ v i ,

( b ) diferença final Δ v f e

( c ) a variação da entropia Δ S do gás?

Passo 1

Olá pessoal, tudo bem? Vamos treinar um pouco de entropia com teoria cinética dos gases? Bora lá?

Da teoria cinética dos gases temos as definições de velocidade provável v p e velocidade quadrática média v r m s :

v p = 2 R T M e v r m s = 3 R T M

O problema pede a diferença entre v p e v r m s , então:

Δ v = v r m s - v p = 3 R T M - 2 R T M ,

ok?

Mas o problema pede a diferença inicial e a final! Mas como assim? É que queremos saber o alargamento de P ( v ) quando a temperatura aumenta, sendo assim temos uma temperatura inicial T i = 250 K e final T f = 500 K .

A constante R vale 8,31 J / m o l . K . E M é a massa molar do nitrogênio que vale 28.10 - 3 k g / m o l

Agora podemos calcular Δ v i e Δ v f !

Passo 2

Para a diferença inicial teremos T i = 250 K , M = 28.10 - 3 k g / m o l , R = 8,31 J / m o l . K . A diferença inicial é:

Δ v i = v r m s - v p = 3 R T i M - 2 R T i M

Δ v i = 3 . 8,31.250 28.10 - 3 - 2 . 8,31.250 28.10 - 3 = 471,79 - 385,21 = 86,6 m / s

Passo 3

Para a diferença final teremos T f = 500 K , M = 28.10 - 3 k g / m o l , R = 8,31 J / m o l . K . A diferença final é:

Δ v f = v r m s - v p = 3 R T f M - 2 R T f M

Δ v f = 3.8,31.500 28.10 - 3 - 2 . 8,31.500 28.10 - 3 = 667,21 - 544,78 = 122,43 m / s

Show! Vamos à definição de entropia?

Passo 4

Logo no começo do enunciado é dito que o gás sofre um aumento de temperatura à volume constante, então o calor envolvido é o calor molar a volume constante.

A fórmula é:

Q = n C V Δ T

Mas não queríamos falar de entropia? Sim! Saca só a definição de variação de entropia:

Δ S = ∫ d Q T

Justamente o diferencial de calor envolvido vai ser :

d Q = n C V d T

Assim Δ S fica:

Δ S = ∫ n C V d T T

E devemos integrar entre as temperaturas T f = 500 K e T i = 250 K .

Mas e o valor de C V ? Lembra que ele tem relação com os graus de liberdade g do gás?

C V = g 2 R

Pois então, o problema fala que o gás é ideal e que ele gira, mas não oscila: isso quer dizer que os graus de liberdade estão restritos a apenas 3 !

Então: C V = 3 2 R = 12,5 J / m o l . K

Show! Agora é só coletar todas essas informações e aplicar na fórmula para a variação de entropia!

Passo 5

A variação de entropia vai ser:

Δ S = ∫ n C V d T T

Δ S = 1,5.12,5 ln ⁡ T f T i  

Δ S = 1,5.12,5 ln ⁡ 500 250 = 12,99 J / K  

Show! Vamos pra próxima?

Resposta

a 86,6 m / s

b 122,43 m / s

( c ) 12,99 J / K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um recipiente de paredes adiabáticas contém 2l de água a 30 ° C . Coloca-se nele um bloco de 500g de gelo. (a) Calcule a temperatura final do sistema. Tome 80c a l / g para o calor latente de fusão do
Um quilograma de gelo é removido de um coneglador a - 15 ° C e aquecido, até converter-se totalmente em vapor, a 100 ° C . Qual é a variação de entropia deste sistema? O calor específico do gelo é de
Um litro de água, inicialmente a 100 ° C , é totalmente vaporizado: (a) em contato com um reservatório térmico a 100 ° C ; (b) em contato com um reservatório térmico a 200 ° C . O calor latente de vap
Dois litros de ar ( γ = 1,4 ), nas condições normais de temperatura e pressão, sofrem uma expansão isobárica até um volume 50 % maior, seguida de um resfriamento a volume constante até baixar a pressã
Um cilindro contendo 1k g de H e a 150a t m , em equilíbrio térmico com o ambiente a 17 ° C , tem um pequeno vazamento através do qual o gás escapa para a atmosfera, até que o tanque se esvazia por co