Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 6.Problemas - Ex. 21

Demonstre que um fóton, propagando-se no vácuo, não pode desintegrar em dois outros, exceto se eles tiverem mesma direção de propagação.

Passo 1

Vamos supor que um fóton se desintegra como mostra a figura abaixo.

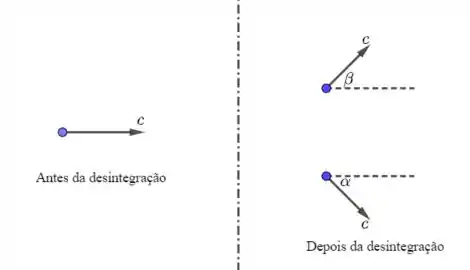
Nesse tipo de problema, devemos conservar:

  1. A energia do sistema;
  2. O momento linear do sistema.

Vamos lá!

Passo 2

Começando conservando a energia.

  1. No início: E i = E 0 ;
  2. No fim: E f = E 1 + E 2 .

Assim, temos

E 0 = E 1 + E 2

Passo 3

Conservando o momento no eixo x:

  • No início: p i x = E 0 / c ;
  • No fim: p f x = E 1 c cos ⁡ β + E 2 c cos ⁡ α

    • Assim,

    E 0 c = E 1 c cos ⁡ β + E 2 c cos ⁡ α E 0 = E 1 cos ⁡ β + E 2 cos ⁡ α

    Conservando o momento no eixo y:

  • No início: p i y = 0 ;
  • No fim: p f y = E 1 c sin ⁡ β - E 2 c sin ⁡ α

Assim,

0 = E 1 c sin ⁡ β - E 2 c sin ⁡ α E 1 sin ⁡ β = E 2 sin ⁡ α

Passo 4

Assim, ficamos com o sistema de equações:

E 0 = E 1 + E 2 E 1 sin ⁡ β = E 2 sin ⁡ α E 1 cos ⁡ β = E 0 - E 2 cos ⁡ α

Elevando as duas últimas equações ao quadrado e somando:

E 1 sin ⁡ β 2 + E 1 cos ⁡ β 2 = E 2 sin ⁡ α 2 + E 0 - E 2 cos ⁡ α 2 E 1 2 sin 2 ⁡ β + cos 2 ⁡ β = E 2 2 sin 2 ⁡ α + E 0 2 - 2 E 0 E 2 cos ⁡ α + E 2 cos 2 ⁡ α E 1 2 = E 2 2 sin 2 ⁡ α + cos 2 ⁡ α + E 0 2 - 2 E 0 E 2 cos ⁡ α E 0 - E 2 2 = E 2 2 + E 0 2 - 2 E 0 E 2 cos ⁡ α E 0 2 - 2 E 0 E 2 + E 2 2 = E 2 2 + E 0 2 - 2 E 0 E 2 cos ⁡ α - 2 E 0 E 2 = - 2 E 0 E 2 cos ⁡ α

Assim, encontramos que cos ⁡ α = 1 ⟹ α = 0 . Da mesma maneira, encontramos que cos ⁡ β = 0 , ou seja, β = 0 ! Logo, devemos ter necessariamente a mesma direção de propagação, como queríamos demostrar.

Resposta

Demonstração.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que a constante de acoplamento para a interação eletromagnética, e 2 / 4 π ϵ 0 ℏ c , é adimensional e possui o valor numérico 1 / 137 .Mostre que, no modelo de Bohr, a velocidade orbital de um
Em qual das seguintes reações a estranheza se conserva? Em cada caso explique seu raciocínio. K + → μ + + ν μ ; n + K + → p + π 0 ; K + + K - → π 0 + π 0 ; p + K - → Λ 0 + π 0 .
Qual das seguintes reações obedece à conservação do número de bárions? p + p → p + e + ; p + n → 2 e + + e - ; p → n + e - + ν - e ; p + p - → 2 γ .
O teor de quark do nêutron é u d d .Qual é o teor de quark do antinêutron? Explique seu raciocínio.O nêutron é sua própria antipartícula? Explique.O teor de quark da partícula ψ é c c - . A partícula
Qual é a energia cinética total dos produtos do decaimento quando uma partícula ípsilon em repouso decai para τ + + τ - .