Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 6.Problemas - Ex. 15

Uma partícula em repouso de massa m 0 se desintegra em duas outras, de massas de repouso m 1 e m 2 . Calcule as energias E 1 e E 2 desses dois fragmentos. Sugestão: Use as leis de conservação e a relação 6.98.

Passo 1

Nesse exercício, vamos usar dois princípios de conservação:

  1. Conservação da energia;
  2. Conservação do momento linear.

Veja a figura abaixo que ilustra a situação.

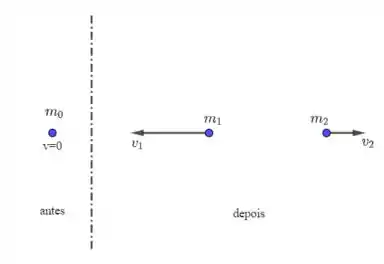
Passo 2

Vamos começar aplicando a conservação da energia.

  • Energia inicial: m 0 c 2 .
  • Energia final: E 1 + E 2 .

    • Assim, temos

    m 0 c 2 = E 1 + E 2

    Passo 3

    Vamos conservar o momento:

  • Momento inicial: p i = 0 .
  • Momento final: p f = E 2 2 c 2 - m 2 2 c 2 - E 1 2 c 2 - m 1 2 c 2

Assim, temos

0 = E 2 2 c 2 - m 2 2 c 2 - E 1 2 c 2 - m 1 2 c 2 E 2 2 c 2 - m 2 2 c 2 = E 1 2 c 2 - m 1 2 c 2 E 2 2 c 2 - E 1 2 c 2 = m 2 2 c 2 - m 1 2 c 2 E 2 2 - E 1 2 c 2 = c 2 m 2 2 - m 1 2 E 2 - E 1 E 2 + E 1 c 2 = c 2 m 2 2 - m 1 2 E 2 - E 1 m 0 c 2 c 2 = c 2 m 2 2 - m 1 2 E 2 - E 1 = c 2 m 2 2 - m 1 2 m 0

Passo 3

Assim, temos:

E 2 + E 1 = m 0 c 2 E 2 - E 1 = c 2 m 2 2 - m 1 2 m 0

Somando essas relações, temos

2 E 2 = c 2 m 0 + m 2 2 - m 1 2 m 0 ∴ E 2 = 1 2 m 0 - m 1 2 - m 2 2 m 0 c 2

Da mesma forma, temos

E 1 = 1 2 m 0 + m 1 2 - m 2 2 m 0 c 2

Resposta

Temos E 2 = 1 2 m 0 - m 1 2 - m 2 2 m 0 c 2 e E 1 = 1 2 m 0 + m 1 2 - m 2 2 m 0 c 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

a) De acordo com a lei de Hubble, qual deve ser a distância r entre a Terra e uma galáxia que se afasta com velocidade igual a c ? b) Explique por que a distancia calculada no item (a) é o tamanho do
Calcule a energia da reação Q (em M e V ) para a reação e - + p → n + v e . Essa reação é endoenergética ou exoenergética?
Calcule a energia liberada em cada uma das seguintes reações:a) p + H 2 → H e 3 ; b) n + H e 3 → H e 4
O pico da radiação do corpo negro de 2,728K ´pssui comprimento de onda igual a 1,062m m . Qual era o comprimento de onda do pico da radiação existente no instante t = 700000 anos quando a temperatura
Calcule a energia liberada (em M e V ) no processo alfa triplo 3 H e 4 → C 12