Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 6.Problemas - Ex. 18

Um fóton de energia E é espalhado por um elétron livre. Demonstre que a máxima energia cinética que o fóton pode transferir ao elétron é dada por

T m á x = E 2 E + 1 2 m c 2

onde m é a massa de repouso do elétron.

Passo 1

A figura abaixo traz um esquema da situação dada no enunciado.

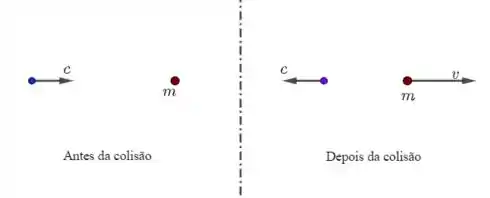
Notemos que, para que haja a máxima transferência de energia cinética para o elétron, o fóton deve “colidir” com o elétron e apenas inverter o sentido de seu movimento (veja a figura!).

Nesse tipo de problema, há duas grandezas que são conservadas:

  • A energia do sistema;
  • O momento linear do sistema.

    • Passo 2

    Vamos começar conservando a energia do sistema.

  • Início: E i = E + m c 2 .
  • Final: E f = E ' + E e , onde E ' é a energia final do fóton e E e é a energia do elétron.

    • Sendo assim, temos

    E + m c 2 = E ' + E e E e = E - E ' + m c 2

    Passo 3

    Agora, vamos conservar o momento linear:

  • Início: p i = E / c .
  • Fim: p f = - E ' c + E e 2 c 2 - m 2 c 2 .

Sendo assim, temos

E c = - E ' c + E e 2 c 2 - m 2 c 2 E + E ' c = E - E ' + m c 2 2 c 2 - m 2 c 2 E + E ' 2 = E - E ' + m c 2 2 - m 2 c 4 E 2 + 2 E E ' + E ' 2 = E 2 + E ' 2 + m 2 c 4 - 2 E E ' + 2 E m c 2 - 2 E ' m c 2 - m 2 c 4 4 E E ' + 2 E ' m c 2 = 2 E m c 2 E ' = E m c 2 2 E + m c 2

Conseguimos, portanto, determinar a energia final do fóton.

Passo 2

Agora, perceba o seguinte: A energia final do elétron será

E e = γ m c 2

Porém, usando o resultado obtido no passo 2:

E - E ' + m c 2 = γ m c 2 E - E ' = m c 2 γ - 1

Porém, m c 2 γ - 1 = T (energia cinética do elétron). Logo,

T = E - E ' T = E - E m c 2 2 E + m c 2 T = 2 E 2 2 E + m c 2 T = E 2 E + 1 2 m c 2

que é o que queríamos provar!

Resposta

Veja a demonstração acima.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Raios cósmicos de mais alta energia são prótons que possuem a energia cinética na ordem de 10 13M e V . (a) Conforme medido no referencial do próton, qual intervalo de tempo um próton com essa quantid
(a) Prepare um gráfico da energia cinética relativística e da energia cinética clássica, ambas como uma função da velocidade, para um corpo com uma massa de sua escolha. (b) A que velocidade a energia
Um elétron possui velocidade de 0,750 c . (a) Encontre a velocidade de um próton que tem a mesma energia cinética do elétron. (b) E se? Encontre a velocidade do próton que tem o mesmo momento de um el
Um corpo de massa 900k g e viajando a 0,850 c de velocidade colide com um corpo em repouso com massa de 1400k g . Os dois corpos se fundem. Determine (a) a velocidade e (b) a massa do corpo composto.
Um astronauta deseja visitar a galáxia de Andrômeda, fazendo uma jornada de ida que levará 30,0a n o s no referencial da nave espacial. Suponha que a galáxia está a 2,00 × 10 6 anos-luz de distância e