Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 3- Ed: 1º - Capítulo 11.Problemas - Ex. 3a

Demonstre que:

  1. A energia armazenada no anel de Rowland (seç.11.8) é 1 2 R   Φ 1 2 , onde R e a relutância magnética e Φ 1 é o fluxho de B através da secção reta;

Passo 1

Vamos lá! O anel que o enunciado refere é esse a seguir, que representa uma bobina toroidal.

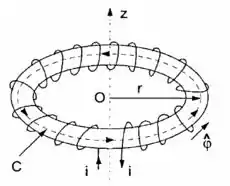
Temos que começar lembrando que a densidade de energia magnética é dada por

u = 1 2 μ B 2

O campo é

B = μ H

onde

H = N i l     .

Substituindo esses valores, podemos escrever a densidade de energia como

u =   1 2 μ μ N i l 2 .

Passo 2

De forma genérica podemos escrever que

Φ 1 = B S = μ N i l S

Portanto, agora podemos escrever a expressão da densidade em função do fluxo

u = 1 2 μ Φ 1 S 2

Passo 3

Sabendo que o volume é dado por

V = l S

Podemos escrever a energia como

U = u V = 1 2 μ Φ 1 S 2 l S

Arrumando a equação, temos

U = 1 2 l μ S Φ 1 2

Passo 4

Sabendo que a relutância é dada por

R = l μ S

Podemos reescrever a energia como

U = 1 2 R Φ 1 2

Resposta

a )   U = 1 2 R Φ 1 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Exercício de Livro
Quando a corrente no Problema 71 [e 0.200 A, o campo magnetico medido [e 1.58 T.Desprezando os efeitos de borda, qual é o campo magnetico aplicado?Qula é a magnetiazção?Qual é a permeabiliade relativa
Exercício de Livro
Exercício de Livro
Exercício de Livro