Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 11.Problemas - Ex. 3b
Demonstre que:
- A autoindutância do anel é .
Passo 1
Vamos lá! Lembra que a autoindutância é dada pela expressão a seguir?
O anel que o enunciado refere é esse a seguir, que representa uma bobina toroidal.
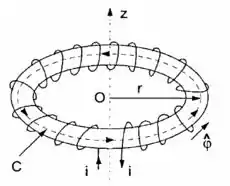
Se liga! Podemos escrever o campo magnético como
onde
Passo 2
De forma genérica podemos escrever que
Como temos N espiras o fluxo será
Portanto, agora podemos escrever a expressão para a autoindutância
Passo 3
Lembrando que a relutância é
Podemos escrever a autoindutância como
Resposta
Exercícios de Livros Relacionados
No circuito magnético da figura, a secção reta é constante, a permeabilidade magnética do material é μ e a corrente na bobina de N espiras é i . Calcule o campo B 1 no braço central e o campo B 2 nos
Demonstre que:A energia armazenada no anel de Rowland (seç.11.8) é 1 2 RΦ 1 2 , onde R e a relutância magnética e Φ 1 é o fluxho de B através da secção reta;
Um anel de Rowland de ferro tem 10 cm de diâmetro médio e nele está aberto um entreferro de 1 mm de comprimento. Quando se faz passar uma corrente de 1 A por uma bobina de 1000 espiras enrolada no ane
A suscetibilidade molar do gás hélio é - 2,4 ⋅ 10 - 11 . Ache a razão do raio quadrático médio r 2 1 / 2 da órtbita eletrônica no átomo de hélio ao raio de Bohr a 0 = 0,0529n m , que é o raio da prime