Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 7.Problemas - Ex. 2
A agulha imantada do problema 1 também produz um campo magnético, que, conforme será visto no capítulo 8, só difere de um dipolo elétrico pelas substituições , , onde é uma constante (permeabilidade magnética do vácuo).
- Usando esse resultado, determine o campo magnético (em módulo, direção e sentido) produzido pela agulha num ponto P situado em seu prolongamento, a uma distância da agulha.
- Suponha que, com a agulha imobilizada na direção horizontal, perpendicular ao campo magnético da Terra, outra agulha imantada é trazida para o ponto definido na parte (a), ficando sujeita aos campos e . Determine o ângulo entre a orientação de equilíbrio da segunda agulha e . Mostre que, medindo-o, pode-se determinar a razão . Combinando o resultado com o do problema 1, obtém-se os valores de e de . Esse método é devido a Gauss.
Passo 1
Para verificar o item (a), precisamos lembrar que o campo elétrico do dipolo elétrico é
Como o enunciado diz que e , podemos fazer as devidas substituições e achar o campo magnético.
Passo 2
Para melhorar nossa compreensão do item (b), podemos ver a figura a seguir.
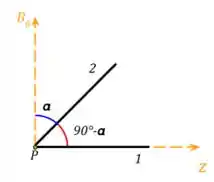
Se liga! Vamos considerar que está em equilíbrio. Então a soma dos torques na agulha 2 tem que ser zero. Sendo os torques provocado pelo campo e pela agulha 1.
Portanto temos que eles produzem torques em sentidos contrários e que os seus módulos são iguais.
Passo 3
Como foi calculado no item (a)
Logo
Agora é só lembrar que
Portanto
Assim achamos que