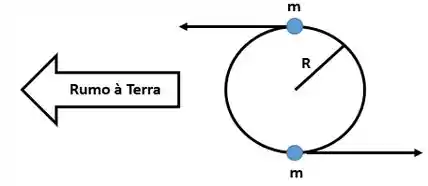
Determinação da massa de uma estrela. Muitas estrelas vistas no céu são na realidade estrelas binárias, ou seja, duas estrelas que giram em torno do centro de massa comum. Quando essas estrelas possuem velocidades angulares elevadas, suas velocidades em relação à Terra podem ser medidas pelo efeito Doppler da luz que elas emitem. As estrelas que se enquadram nessa caso denominam-se estrelas binárias espectroscópicas. Na figura 37.30 mostramos um caso simples de estrelas binárias espectroscópicas: duas estrelas idênticas, cada uma delas com massa , giram em torno de centro de massa comum descrevendo uma circunferência de raio R. O plano comum das órbitas das estrelas é visto de perfil em relação a um observador na Terra

1. A luz produzida pelo gás hidrogênio em um laboratório na Terra possui frequência iguala . Observamos através de um telescópio na Terra que a luz proveniente dessas estrelas possui uma frequência que varia entre e . Verifique se esse sistema binário se aproxima e se afasta da Terra, calcule a velocidade do sistema e a velocidade angular das estrelas. (Sugestão: as velocidades envolvidas são muito menores do que a velocidade da luz, de modo que você pode usar o resultado aproximado dado na Seção 37.6
2. A frequência da luz proveniente de cada estrela no sistema binário varia desde um valor máximo até um valor mínimo e retorna ao valor máximo em um período igual a . Determine o raio orbital e massa de cada estrela. Forneça a resposta da massa em quilogramas e tabém como um múltiplo da massa do Sol . Compare o valor de R com a distância entre a Terra e o Sol (Essa técnica é efetivamente usada na astronomia para a determinação da massa de estrelas. Na prática, o problema é mais complicado porque em um sistema binário as estrelas não costumam ser idênticas, as órbitas geralmente não são circulares e o plano da órbita está inclinado em relação à linha de visão de um observador na Terra.)

Passo 1

Resposta