Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 5
Em um dia de inverno gelado, o coeficiente de atrito entre os pneus de um carro e uma estrada é reduzido para um quarto de seu valor em um dia seco. Como resultado, a velocidade máxima na qual o carro pode percorrer com segurança uma curva de raio é reduzida. O novo valor para esta velocidade é
(a)
(b)
(c)
(d)
(e) reduzida de uma quantidade desconhecida que depende da massa do carro.
Passo 1
Olá, tá bem? Então, ele diz que temos um carro fazendo uma curva. E ele quer saber a relação entre a velocidade máxima dele em dia normal e um dia de inverno, sabendo que o coeficiente de atrito no dia de inverno é ¼ do dia normal.
Esse movimento de passar na curva é o pedacinho de um movimento circular de rapidez constante :
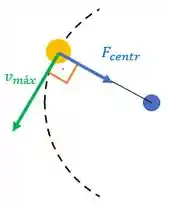
Para que o carro se mantenha nessa trajetória circular, é necessário que acha uma força centrípeta. Quem faz esse papel?
Primeiro, temos que saber quais são as forças que agem no carro em uma estrada, e essas forças são: força normal, força peso e força de atrito. A força que faz o papel de força centrípeta é a força que vai ser a força de atrito. Ela vai apontar para o centro da trajetória do carro.
O arranjo dessas forças está representado abaixo:
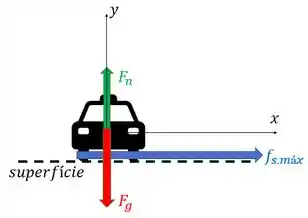
Porém, a força de atrito tem que ter o mesmo valor da força centrípeta para o carro “não sair pela tangente” (sair da trajetória circular). A força centrípeta é:
Em que é a massa do carro, é a velocidade máxima que o carro pode fazer a curva e é o raio da curva.
Passo 2
Aplicando a segunda lei de Newton para a direção vertical vamos ter
Só que o carro não sobe nem desce, então .
O somatório de forças na vertical é porque está no sentido negativo de , assim substituindo isso na lei:
Como :
Passo 3
A gente pode lembrar que se a velocidade é máxima, a força de atrito que vai ser a centrípeta também é máxima.
Como ela é perpendicular ao movimento (por ela ser uma força centrípeta), na direção dela não há movimento. Nesse caso temos o atrito estático que tem como expressão para a magnitude máxima:
Mas a gente viu que :
Como a força de atrito deve ser igual a força centrípeta, podemos igualar as expressões de e
Achamos uma expressão para em função do coeficiente de atrito .
Passo 4
Para o dia fora do inverno o coeficiente de atrito entre a estrada os pneus é e a velocidade máxima é . Assim a relação entre essas duas grandezas é:
Mas nós chamaremos o coeficiente de atrito para o dia de inverno gelado, e consequentemente, nesse dia a velocidade máxima é . Então a relação entre esses dois caras fica:
Dividindo a velocidade máxima no dia de inverno gelado com a velocidade máxima em dia seco para termos uma relação entre elas, temos:
Como o enunciado disse, que o coeficiente e atrito no inverno é ¼ do dia sem inverno, escrevemos que . Substituindo isso ali em cima e simplificando:
Resposta
Resposta correta: (c)