Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 18.1 - Ex. 81

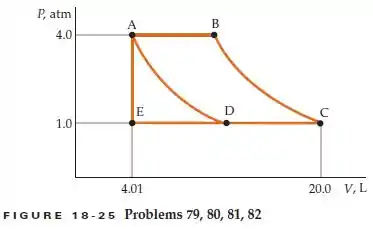
O diagrama PV da Figura 18-25 representa 3,00 mol de um gás monatômico ideal. O gás está inicialmente no ponto A. Os caminhos AD e BC representam variações isotérmicas. Se o sistema é conduzido ao ponto C ao longo do caminho ADC, determine:

  1. As temperaturas inicial e final do gás;
  2. O trabalho realizado pelo gás;
  3. O calor absorvido pelo gás.

Passo 1

Essa é bem tranquilinha! Queremos na letra a as temperaturas iniciais e finais, e se você observar atentamente, nós temos todas as variáveis necessárias para calculá-las. Basta usarmos a lei dos gases:

P A V A = n R T A

E neste caso, T A é a temperatura inicial do gás. Isolando:

T A = P A V A n R

Substituindo:

T A = 4   a t m   x 101325   P a a t m 4,01   L   x 10 - 3 m 3 L 3   m o l s . 8,314 J m o l . K = 65,2   K

E o ponto final do processo será C, então a temperatura final será T C . Calculada do mesmo jeito:

T c = 1   a t m   x 101325   P a a t m 20   L   x 10 - 3 m 3 L 3   m o l s . 8,314 J m o l . K = 81,2   K

Finalizamos uma, bora pra próxima!

Passo 2

Na letra b queremos saber o trabalho realizado pelo gás. O trabalho total será:

W t o t a l = W A → D + W D → C

No caminho D → C o processo ocorre a pressão constante. Então o trabalho é calculado por:

W D → C = P . ∆ V = P ( V C - V D )

Não temos V D , mas já sabemos como calculá-lo:

V D . P D = n R T D

Como o processo de A → D ocorre a temperatura constante,

T D = 65,2   K

Isolando V D :

V D . 1   a t m   x 101325   P a a t m = 3   m o l s . 8,314 J m o l . K ( 65 , 2   K )

V D = 0,016   m ³ = 16   L

Substituindo no trabalho:

W A → D = 1   a t m   x 101325   P a a t m . 20   L - 16   L x 10 - 3 m 3 L

W A → B = 0,4   k J

No caminho A → D , temos um processo isotérmico. Neste caso o trabalho é calculado como:

W B → C = n R T . ln ⁡ V D V A

Substituímos:

W B → C = 3   m o l s . 8,314 J m o l . K 65,2   K . ln ⁡ 16   L 4,01   L

W B → C = 2,25   k J

Sendo assim, o trabalho total será:

W t o t a l = 2,25   k J + 0,4 k J = 2 , 7   k J

Passo 3

Na letra c queremos o calor absorvido ao longo deste caminho. Pela primeira lei:

∆ E i n t = Q + W s o b r e   o   g á s

Nós acabamos de calcular o trabalho feito pelo gás e sabemos que se relaciona com o trabalho sobre o gás da seguinte forma:

W s o b r e   o   g á s = - W p e l o   g á s = - 2 , 7   k J

Mas ainda não temos a variação da energia. Mas é fácil! Também temos uma fórmula para ela:

∆ E i n t = g 2 n R ∆ T

Onde g são os graus de liberdade. Para um gás monoatômico, g = 3 :

∆ E i n t = 3 2 n R ( T c - T A )

Substituindo os dados na fórmula:

∆ E i n t = 3 2 3   m o l s . 8,314 J m o l . K . 81,2   K - 65,2 K = 0,6   k J

Jogando na fórmula da primeira lei:

0,6   k J = Q - 2 , 7   k J

Q = 3,3   k J  

Resposta

  1. T A = 65,2   K   e   T C = 81,2   K ;
  2. W t o t a l = 2,7   k J ;
  3. Q = 3 , 3   k J .  
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No Problema FE9.3, se a área na seção 1 é 0,15m2 , qual é a vazão em massa?(a) 38,1 kg/s, (b) 53,6 kg/s, (c) 57,8 kg/s, (d) 67,8 kg/s, (e) 77,2 kg/s
Para escoamento isentrópico permanente, se a temperatura absoluta aumenta 50%, em qual razão a pressão estática aumenta?(a) 1,12, (b) 1,22, (c) 2,25, (d) 2,76, (e) 4,13
Na Figura FE9.6, se não há ondas de choque e a pressão em uma seção do duto é de 55,5 kPa, qual é a velocidade nessa seção ?(a) 166 m/s, (b) 232 m/s, (c) 554 m/s, (d) 706 m/s, (e) 774 m/s
Para escoamento isentrópico permanente, se a densidade duplica, em qual razão a pressão estática aumenta?(a) 1,22, (b) 1,32, (c) 1,44, (d) 2,64, (e) 5,66
No Problema FE9.3, qual é a temperatura na seção 1?(a) 300 K, (b) 408 K, (c) 417 K, (d) 432 K, (e) 500 K