Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 13.1 - Ex. 60

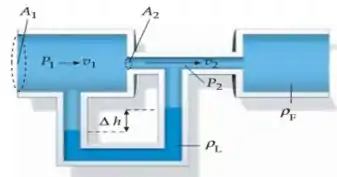
A água flui através de um tubo de Venturi, com um diâmetro d 1 = 9,50 c m e um diâmetro de constrição d 2 = 5,60 c m . O manômetro com tubo em forma de U está parcialmente preenchido com mercúrio. Encontrar a taxa de vazão da água I v para uma diferença no nível de mercúrio h = 2,40 c m .

Passo 1

Usando a definição de vazão, temos que:

I v = A 1 v 1

Lembrando que:

A 1 = π r 1 2

Então, temos:

I v = π r 1 2 v 1

Passo 2

Como o problema se trata de um tubo de Venturi, é válido lembrar que a equação de rege a velocidade de fluxo v 1 com que o fluído chega ao tubo é dada por:

v 1 = 2 ( p L - p F ) g h p F ( r 1 2 r 2 2 - 1 )

Sendo, nessa questão:

p L = 13,6.10 3 k g / m 3 (densidade do mercúrio)

p F = 1.10 3 k g / m 3 (densidade da água)

Como: r = d 2

Vamos substituir na equação:

v 1 = 2 ( p L - p F ) g h p F ( d 1 2 4 d 2 2 4 - 1 )

v 1 = 2 ( p L - p F ) g h p F ( d 1 2 d 2 2 - 1 )

Passo 3

Por fim, vamos unir as duas equações encontradas:

I v = π r 1 2 v 1

v 1 = 2 ( p L - p F ) g h p F ( d 1 2 d 2 2 - 1 )

Que nos fornece a seguinte igualdade:

I v = π d 1 2 4 2 ( p L - p F ) g h p F ( d 1 2 d 2 2 - 1 )

Agora vamos aplicar os valores fornecidos:

I v = π 0,095 2 4 2 13,6.10 3 - 1.10 3 ( 9,81 ) ( 0,024 ) 1.10 3 ( 0,095 0,056 2 - 1 )

I v = 0,01258 m 3 / s

I v = 13 L / s

Resposta

I v = 13 L / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Deduza a Equação (14.12). b) Quando a densidade cresce 1,50 % de um ponto 1 até um ponto 2, o que ocorre com a vazão volumétrica?
A água escoa em um tubo cuja seção reta possui área variável e enche completamente o tubo em todos os pontos. No ponto 1, a seção reta possui área igual a 0,070 m 2 e o modulo da velocidade do fluido
A água escoa em um tubo cilíndrico cuja seção reta possui área variável. A água enche completamente o tubo em todos o spontos. a) Em um ponto o raio do tubo é igual a 0,150m. Qual é a velocidaded da á
Uma cabeça de chuveiro possui 20 aberturas circulares, cada uma com raio de 1,0 mm. A cabeça de chuveiro é conectada a um cano de raio igual a0,80 cm. Se a velocidade da água no cano é 3,0m/s, qual é
Uma mangueira de incêndio deve poder lançar água no topo de um prédio de 35,0m de altura quando apontada para cima. A água entra na mangueira a uma taxa constante de 0,500 m 3 / s e sai por um esguich