Na difração de fenda simples de Fraunhofer, o padrão de intensidade (Figura 33-11) consiste em um máximo central largo com uma sequência de máximos secundários de cada lada do máximo central. A intensidade é dada por , onde é a diferença de fase entre as ondas secundárias chegando das extremidades opostos das fendas. Calcule os valores de para os primeiros três máximos secundários de um lado do máximo central determinando os valores de para os quais é igual a zero. Confira seus resultados comparando suas respostas com valores aproximados para igual a , e . (Na discussão sobre a Figura 33-27 será mostrado que estes valores de são aproximadamente corretos nos máximos de intensidade secundários.)
Passo 1
Olá pessoal, tudo certo com vocês? Espero que sim 😊. Vamos entender melhor essa questão?
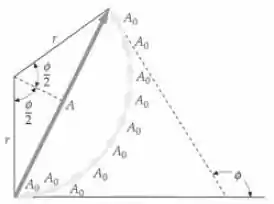
Certo! Observe que, podemos usar o diagrama de fases mostrado na Figura abaixo para determinar os três primeiros valores de que produzem máximos de intensidade secundária. Definindo a derivada da Equação igual a zero produzirá uma equação transcendental cujas raízes são os valores de que correspondem aos máximos de intensidade no padrão de difração.
Passo 2
Certo! Atentando-se a figura do passo anterior, vemos que o primeiro máximo subsidiário ocorre onde:
A intensidade mínima ocorre quanto:
Outra intensidade máxima ocorre quanto
Assim, os máximos de intensidade secundária ocorrem onde:
e os três primeiros máximos de intensidade secundária estão em e .
Passo 3
A intensidade no padrão de difração de uma única fenda é dada por:
Definindo a derivação desta expressão igual a zero para valores extremos (mínimos e máximos relativos):
Simplificando a equação, vamos obter que
Resolva esta equação numericamente (use a função ″Solver″ de sua calculadora ou métodos de tentativa-e-erro) para obter:
e
Nos três mínimos de intensidade e , e nos três máximos de intensidade e . Na intensidade máxima e .
Passo 4
Observe que nossos resultados no Passo 3 são menores do que os valores aproximados encontrados no Passo 2 em , e e que o acordo melhora conforme aumenta.
Passo 5
Pronto! Finalizamos a questão 😊. Nos vemos na próxima questão. OK? Até mais.
Resposta
e
e