Luz com comprimento de onda de incide normalmente em quatro fendas. Cada fenda tem de largura e a separação centro a centro entre ela e a próxima fenda é . (a) Determine a largura angular do máximo central de intensidade do padrão de difração de fenda simples em um anteparo distante. (b) Determine a posição angular de todos os máximos de interferência que estão no interior do máximo central de difração. (c) Determine a largura angular do máximo central de interferência. Isto é, determine o ângulo entre os primeiros mínimos de interferência de cada lado do máximo central de interferência. (d) Faça um esboço da intensidade relativa como função do seno do ângulo.
Passo 1
Olá pessoal, tudo certo com vocês? Espero que sim 😊. Vamos entender melhor essa questão?
Certo! Observe que, podemos usar para encontrar os primeiros zeros na intensidade padrão. Os máximos de interferência de quatro raios ocorrem nos ângulos dados por , onde . Em (c), podemos usar o resultado do Problema 53 para encontrar a distribuição angular entre a interferência central máxima e a primeira interferência mínima em ambos os lados da mesma. Em (d) usaremos um diagrama de fases para um grade de quatro ranhuras para encontrar a amplitude resultante em um determinado ponto da intensidade padrão em função da constante de fase , que, por sua vez, é uma função do ângulo que determina a localização de um ponto no padrão de interferência.
Passo 2
Certo! Os primeiros zeros na intensidade ocorrem nos ângulos dados por:
Substituindo numericamente os valores, encontraremos que
Passo 3
Já no item b) Os máximos de interferência de quatro raios ocorrem nos ângulos dados por:
onde,
Substituindo numericamente, temos
Avaliando para
onde não será visto como coincidindo com o primeiro mínimo no padrão de difração.
Passo 4
Já estamos quase terminando. Para o item d) vamos usar o método de fasor para mostrar a superposição de quatro ondas da mesma amplitude e diferença de fase constante .
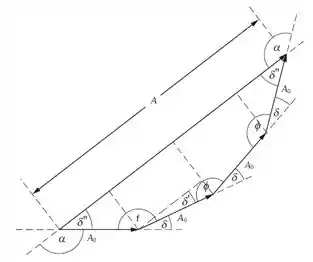
Assim, vamos expressar em termos de e :
Como a soma dos ângulos externos de um polígono é igual a , temos:
Examinando o diagrama de fases, vemos isso:
Eliminar α e resolver para para obter:
Como a soma dos ângulos internos de um polígono de lados é , temos:
A partir da definição de um ângulo reto que temos:
Eliminamos entre estas equações para obter:
Substituir δ '' e δ '' na equação de vamos obter:
Como a intensidade é proporcional ao quadrado da amplitude da onda resultante, encontraremos
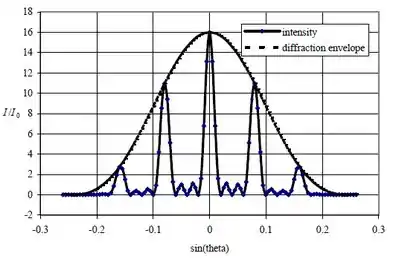
O seguinte gráfico do em função do foi plotado utilizando uma planilha. O envelope de difração foi traçado usando , onde . Note o excelente acordo com os resultados calculados em (a), (b) e (c).
Passo 5
Pronto! Finalizamos a questão 😊. Nos vemos na próxima questão. OK? Até mais.