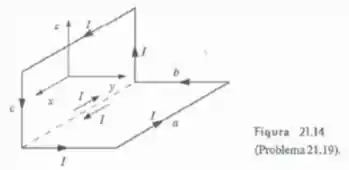
Dipolo magnético de circuitos não-planos. Calcule o dipolo magnético do circuito não-plano mostrado na Figura 21.14. Sugestão: imagine o circuito compostos por dois circuitos planos e retangulares, que se completam pela linha tracejada.

Fala pessoal, beleza?

Para resolver esse problema vamos seguir o mesmo espírito do item (a) do último exercício (21.18) e a sugestão dada no enunciado.

Primeiro eu tenho que convencer vocês que a gente pode olhar para circuito completo como se fossem dois circuitos retangulares planos, um no plano e outro no plano . Os dois circuitos se encontram na linha tracejada transportando correntes em sentidos contrários de modo que elas se anulam. Desta forma, esse conjunto de dois circuitos é equivalente ao circuito completo da figura.

O dipolo magnético do retângulo no plano será

A direção do vetor dipolo é normal ao plano do retângulo. Desta forma, para o retângulo no plano , temos