Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 23.Exercícios e Problemas - Ex. 4

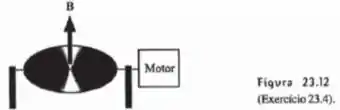
O campo magnético em uma região do espaço é homogêneo e tem valor B = 0,10   T . Um anel circular de raio igual a 10   c m , situado nessa região, gira em torno de um eixo contido em seu plano, passando pelo seu centro. Tal eixo é ortogonal ao campo B , como mostra a Figura 23.12. O anel gira com a frequência de 60   H z , e sua resistência vale 0,50   Ω . Calcule: (a) a variação temporal da corrente elétrica no anel; (b) a potência média realizada pelo motor que gira o anel.

Passo 1

O fluxo magnético sobre o anel será dado pelo produto escalar do campo magnético com o vetor área do anel:

Φ B = B → ⋅ n ^   A

O ângulo entre os dois vetores será dado por

ϕ = ω t = 2 π f t

Assim,

Φ B = B A cos ⁡ ϕ = B A cos ⁡ 2 π f t

Como A = π R 2 , temos que

Φ B = π B r 2 cos ⁡ 2 π f t

Passo 2

Para encontrar a fem, vamos usar a lei de Faraday:

E = - d Φ B d t = - π r 2 B ⋅ d d t cos ⁡ 2 π f t

Assim,

E = π r 2 B ⋅ 2 π f ⋅ s e n   2 π f t = 2 π 2 r 2 B f   s e n   2 π f t

Para achar a corrente, usamos

E = R I → I = E R = 2 π 2 r 2 B f R   s e n   2 π f t

Já para a potência, usamos

P = R I 2 = R ⋅ 4 π 4 r 4 B 2 f 2 R 2   s e n 2 2 π f t

Portanto,

P = 4 π 4 r 4 B 2 f 2 R   s e n 2 2 π f t

Para achar o valor médio temporal, usamos que

s e n 2 2 π f t = 1 2

Assim,

P = 4 π 4 r 4 B 2 f 2 R ⋅ 1 2

Ou ainda,

P = 2 π 4 r 4 B 2 f 2 R

Resposta

I = 2 π 2 r 2 B f R   s e n   2 π f t

P = 2 π 4 r 4 B 2 f 2 R

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um solenoide cilíndrico contendo 200 espiras tem comprimento de 20c m e diâmetro de 3,0c m . Um anel com diâmetro de 2,0c m está situado no centro do solenoide, posicionado de forma coaxial com ele. A
Uma célula fotovoltaica é baseada no GaAs, sujas bandas de valência e de condução estão separadas pela energia E g = 1,42e V . A célula é iluminada com luz vermelha, cujos fótons têm energia h ν = 1,9
Um fio de cobre de diâmetro igual a 0,50m m é utilizado para a fabricação de um solenoide com comprimento de 17c m , contendo 300 espiras de raio igual a 2,0c m . Utilizando os resultados obtidos no 2
Calcule a divergência e o rotacional do campo complexo E → x ,y ,z = E → 0e ik → ⋅ r → , onde E → 0 e k → são vetores constantes.
Sendo f r → e V → r → , respectivamente, um campo escalar e um campo vetorial, mostre que ∇ ⋅ f V → = f∇ ⋅ V → + V → ⋅ ∇ f