Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 26.1 - Ex. 60

Um disco fino não-condutor e não-uniforme tem massa m , raio R e carga total Q , com carga por unidade de área σ variando de acordo com σ 0 r / R , e massa por unidade de área de σ m que é dada por m Q ⋅ σ . O disco gira com rapidez angular ω em torno de seu eixo central.

a Mostre que o momento magnético do disco tem magnitude 1 5 ⋅ π ⋅ ω ⋅ σ 0 ⋅ R 4 , que pode ser reescrito como 3 10 ⋅ ω ⋅ Q ⋅ R 2 .

b Mostre que o momento magnético μ → e o momento angular L → estão relacionados por μ → = 1 2 ⋅ Q m ⋅ L → .

Passo 1

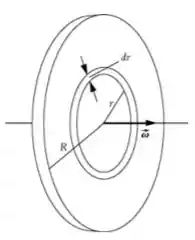
Fala aí bonit@s, como vocês estão? Prontos pra mais uma questão bacana?Se liguem só no que a gente vai fazer pra matar esse problema de uma vez por todas. Pois bem podemos expressar o momento magnético de um elemento de corrente d I devido a um anel de raio r , e espessura d r com carga d q . Integrar essa expressão de r   =   0   a   r   =   R nos dará o momento magnético do disco. Podemos integrar a carga no anel entre esses mesmos limites para encontrar a carga total no disco e dividir µ por Q para estabelecer a relação entre eles. Na Parte ( b ) , podemos encontrar o momento angular do disco encontrando primeiro o momento de inércia do disco integrando r 2   d m entre os mesmos limites usados acima. Desenhando essa situação ficamos com o seguinte esboço

Passo 2

Para o primeiro item, temos que o momento magnético para um elemento do disco pode ser expresso como

d μ = A d I         1

Onde a área é dada por

A = π ⋅ x 2     2

Também podemos expressar nosso elemento de corrente da seguinte forma

d I = d q ∆ t = σ d A ∆ t = f σ d A = ω 2 π ⋅ σ 0 ⋅ r R ⋅ 2 π r d r = σ 0 ω R ⋅ r 2   d r       3

Substituindo 2   e   3 em 1 vamos obter

d μ = π r 2 ⋅ σ 0 ω R ⋅ r 2   d r     = σ 0 ⋅ π ⋅ ω R ⋅ r 4   d r      

Agora, integrando a expressão acima de r = 0   a t é   r = R teremos

μ = σ 0 ⋅ π ⋅ ω R ⋅ ∫ 0 R r 4 d r = 1 5 ⋅ σ 0 ⋅ π ⋅ ω ⋅ R 4         4

Por outro lado, temos que a carga d q dentro de uma distância r do centro do disco é dada por

d q = 2 π r σ d r = 2 π r ⋅ σ 0 ⋅ r R d r = 2 π σ 0 R ⋅ r 2   d r

Integrando de r = 0   a t é   r = R também, vamos obter

Q = 2 π σ 0 R ∫ o R r 2 d r = 2 3 ⋅ π σ 0 R 2     5

Agora, dividindo 4 por ( 5 ) vamos ficar com

μ Q = 1 5 ⋅ σ 0 ⋅ π ⋅ ω ⋅ R 4 2 3 ⋅ π σ 0 R 2 → μ = 3 10 ⋅ Q ω R 2

Com isso, mostramos que as duas relações são equivalentes.

Passo 3

Para o item b vamos expressar o momento de inércia de um elemento de massa d m do disco como

d I = r 2   d m = r 2 σ m d A

d I = r 2 ⋅ m Q ⋅ σ ⋅ 2 π r   d r

d I = 2 π m σ 0 Q R ⋅ r 4 d r  

Integrando a expressão acima em ambos os lados vamos obter

I = 2 π m σ 0 Q R ⋅ ∫ 0 R r 4   d r = 2 π m σ 0 R 4 5 Q  

Agora, vamos dividir a expressão 5 do item anterior pela expressão acima de modo que obteremos

I Q = 2 π m σ 0 R 4 5 Q 3 10 ⋅ Q ω R 2 → I = 3 m 5 ⋅ R 2

Temos que o momento angular do disco pode ser expresso como

L = I ω = 3 5 ⋅ m R 2 ω

Para finalizar nosso problema, vamos dividir a expressão 4 do item anterior pela expressão acima de modo a obter

μ L = 1 5 ⋅ σ 0 ⋅ π ⋅ ω ⋅ R 4 3 5 ⋅ m R 2 ω → μ → = Q 2 m ⋅ L →

Prontinho, está concluído nosso exercício sem muitos problemas só um pouquinho de conta.

Resposta

a   D e m o n s t r a ç ã o

b   D e m o n s t r a ç ã o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. 28-48 mostra uma espira ABCDEFA percorrida por uma corrente i = 5,00 A . Os lados da espira são paralelos aos eixos coordenados, com A B = 20,0 c m , B C = 30,0 c m e F A = 10,0 c m . Em termos
A Fig. 28-51 mostra a energia potencial U de um dipolo magnético na presença de um campo magnético externo B em função do ângulo ϕ entre a direção de B e a direção do dipolo magnético. A escala do eix
A Terra possui um momento dipolar magnético de 8,0 ⋅ 10 22J / T . (a) Que corrente teria que existir em uma única espira de fio estendida na superfície da Terra ao longo do equador geomagnético para c
Uma carga q está distribuída uniformemente ao longo de anel delgado de raio r . O anel está girando com velocidade angular ω em torno de um eixo que passa pelo centro e é perpendicular ao plano do ane
A agulha de uma bússola, com 0,050k g de massa e 4,0c m de comprimento, está alinhada com a correspondente horizontal do campo magnético da Terra em um local onde a componente tem o valor B h = 16μ T