A intensidade do pólo de um ímã em barra é definida como , onde é o momento magnético do ímã e é a posição do pólo norte do imã em relação ao pólo sul. Mostre que o torque exercido em um ímã em barra em um campo magnético uniforme é o mesmo que para o caso de uma força exercida sobre o polo norte e uma força exercida sobre o polo sul.

E aí bonit@s, tudo bem com vocês?

Olha só, a questão fala de ímã, polo Norte, polo Sul e pra não confundir nossa cabeça vamos desenhar um esquemático do problema

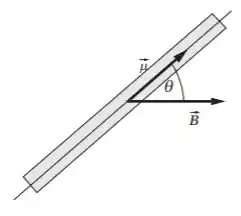
Vamos assumir que uma força é exercida na extremidade do polo norte e uma força é exercida na extremidade do polo sul e mostrar que esta suposição leva à expressão familiar para o torque que atua em um dipolo magnético. Sendo assim, teremos que o torque que atua sobre o ímã da barra dado por

Substituindo o valor de encontramos

Ainda podemos reescrever a expressão acima como sendo

E pronto, acabamos o problema. Cê acredita?