Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 9

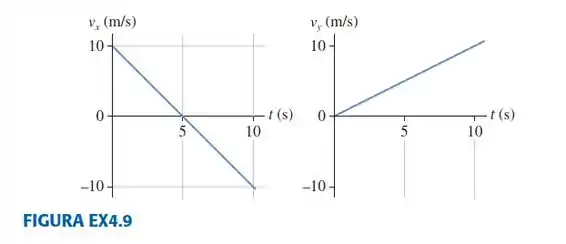
9 . || Um disco de hóquei movido a foguete move-se sobre uma mesa horizontal sem atrito. A F I G U R A   E X 4.9 mostra os gráficos de v x e de v y , os componentes   x   e   y   da velocidade do disco. Ele parte da origem.

a . Qual é o módulo da aceleração do disco?

b . A que distância da origem ele se encontra em t   = 0 s , 5 s e 10 s ?

Passo 1

Nessa precisamos lembrar das representações de um número no plano cartesiano, veja:

Nós podemos achar o pontinho de várias formas:

G r á f i c a : ( x , y )

V e t o r i a l   : a i ^ + b j ^

R e t a n g u l a r :   x + j y

P o l a r : r ∠ θ    

E x p o n e n c i a l : r e j θ

Essas formas se comunicam entre si, e ainda podemos estender isso adicionando um terceiro eixo.

Nessa questão, e na maioria, vamos usar forma vetorial e a forma polar.

Temos essa relação de conversão entre vetorial e polar:

r = a 2 + b 2

θ = tan - 1 ⁡ b a  

Passo 2

a . Qual é o módulo da aceleração do disco?

Lembre-se que:

A aceleração é a derivada da velocidade.

Observe que a variação da velocidade é retilínea, isso é a aceleração será constante em qualquer ponto, isso nos permite usar a derivada com uma subtração simples. Acompanhe:

Vamos analisar pela decomposição em x e y

a x = d v x d t = ( - 10 - 10 ) ( 10 - 0 ) = - 2 m / s 2

a y = d v y d t = ( 10 - 0 ) ( 10 - 0 ) = 1 m / s 2

Logo o módulo será:

a = a x 2 + a y 2 = - 2 2 + 1 2  

a = 2,2 m / s 2

Passo 3

b . A que distância da origem ele se encontra em t   = 0 s , 5 s e 10 s ?

Já sabemos que disco está com o disco está passando por aceleração constante nas direções x e y , quando ele tem esse comportamento, ele descreve uma parábola, e tem essa fórmula bem conhecida da cinemática:

Δ s = v 0 t + 1 2 a t 2  

Podemos reescreve-la:

s 1 - s 0 = v 0 t + 1 2 a t 2

s 1 = + s 0 + v 0 t + 1 2 a t 2

Agora podemos aplica-la para decomposição de x e y :

Para x :

x 1 = + x 0 + v 0 x t + 1 2 a x t 2

x 1 = + 0 m + ( 10 m / s ) t + 1 2 ( - 2 m / s 2 ) t 2

Para y :

y 1 = + y 0 + v 0 y t + 1 2 a y t 2

y 1 = + 0 m + ( 0 m / s ) t + 1 2 ( 1 m / s 2 ) t 2

y 1 = + 0 m + 0 m + 1 2 ( 1 m / s 2 ) t 2

Com isso temos que o módulo vai ser:

s = x 1 2 + y 1 2  

s = 10 t + 1 2 - 2 t 2 2 + 1 2 ( 1 ) t 2 2

Pronto, agora achamos a posição para cada tempo solicitado. Chegamos a essa tabelinha aqui:

Resposta

( a )

a = 2,2 m / s 2

( b )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Não é possível ver corpos muito pequenos, tais como vírus, utilizando um microscópio de luz comum. No entanto, em um eletrônico, podemos vê-los usando um feixe de elétrons em vez de um feixe de luz. A
O “Cometa Vômito”. Em treinamento de astronautas e testes de equipamento em microgravidade, a Nasa faz voar uma aeronave KC135A ao longo de uma trajetória parabólica de voo. Como mostrado na Figura P3
Considerando os vetores do exercício 3.2, (A) Calcule a ^ , b ^ e a ^ × b ^ ; (B) os vetores a ^ × b ^ e a × b a × b são iguais? Explique.
Sejam os vetores a = 5 i + 7 j e b = - 3.5 i + 6 k . Calcule (A) o ângulo entre a e b. (B) o produto escalar a ⋅ b . (C) o produto vetorial a × b e (D) e vetor c = 2 a - 3 b
Calcule o produto tensorial a b entre os vetores a = 2 i + j + 3 k e b = 3 i + 2 j + 2 k .