Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 3.Problemas - Ex. 45
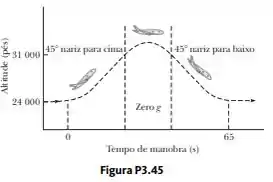
O “Cometa Vômito”. Em treinamento de astronautas e testes de equipamento em microgravidade, a Nasa faz voar uma aeronave KC135A ao longo de uma trajetória parabólica de voo. Como mostrado na Figura P3.45, a aeronave sobe de 24000 pés para 31000 pés, onde entra em uma trajetória parabólica com velocidade de 143 m/s com o nariz para cima a 45,0° e sai com velocidade 143 m/s a 45,0° e o nariz para baixo. Durante essa parte do voo, a aeronave e os objetos dentro da cabine acolchoada estão em queda livre; os astronautas e o equipamento flutuam livremente como se não houvesse gravidade. Qual é (a) a velocidade da aeronave e (b) sua altitude no topo da manobra? (c) Qual é o intervalo de tempo passado na microgravidade?
Passo 1
(a)Amores, pra gente saber a velocidade do avião, na horizontal, a gente pode usar um esqueminha usado muito já em outras questões aqui no capítulo, de lançamentos oblíquos.
É esse aqui:
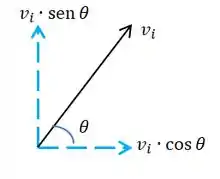
Bom, como a velocidade de subida da aeronave é de 143 m/s, e como a gente conhece o ângulo de subida com a horizontal, sendo , a velocidade na horizontal se determina facinho:
A gente vai ter, nesse caso:
Passo 2
(b) Então, no que chega à altura de pés, o avião sobe um pouco mais, em movimento parabólico, atingindo a altura , do vértice da parábola.
Vamos analisar o movimento vertical do avião pra esse caso. A gente determinou no Passo 1 a velocidade horizontal, e agora a gente precisa da velocidade vertical que ele teve, iniciando a subida até o pico , usando o mesmo esquema. A gente vai ter:
No caso, pelo ângulo de , era de se esperar que fosse a mesma velocidade, ok?
Tá. Agora, como na zona de gravidade zero o avião entra em queda livre (como se desligasse os motores), a gente tem como calcular a altura máxima a que ele chega, uma vez que, na vertical, ele vai ter velocidade nula, nessa altura máxima.
Calculamos pela equação de Torricelli, a melhor pra gente nesse momento. Essa daqui:
Aqui a gente vai ter , , é a gravidade e , o deslocamento até o do vértice da parábola, beleza?
Aqui a gente vai ter:
Aqui a gravidade leva sinal negativo uma vez que a gente está avaliando um movimento de subida do avião, beleza? Seguindo em frente, temos:
Com isso, gente a altura alcançada pelo avião vai ser a soma dos pés e de , que foi a altura atingida pelo avião durante a manobra, tendo então:
Passo 3
Agora, queridos, pra saber o tempo passado na zona de gravidade zero, a gente pode fazer isso por calcular o tempo de queda do avião até retornar a descida retilínea, como visto no gráfico.
Dá pra fazer isso pela fórmula do sorvetão, aqui:
Aqui, no caso, vale o deslocamento do avião desde o pico máximo na manobra até a altura de 31000 pés de novo, que no caso vale , como a gente calculou ainda agora.
Beleza, e a velocidade inicial , na vertical, sendo uma queda, é nula, certo?
A aceleração é também a gravidade e o nosso objetivo é determinar o tempo .
Aplicando os nossos dados, a gente tem o seguinte:
Nisso, determinamos:
Só queee, como falamos no começo, esse é o tempo só da queda!
Em exercícios anteriores a gente já viu que, pra esses casos de lançamento oblíquo, o tempo de queda é igual ao tempo de subida. Logo, o tempo total dentro da zona de gravidade zero vai ser o dobro disso!
Vai valer:
Resposta
(a)
(b)
(c)