Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 9
Um disco é livre para girar em torno de um eixo fixo. Uma força tangencial, aplicada a uma distância do eixo, produz uma aceleração angular . Qual é a aceleração angular produzida se a mesma força é aplicada a uma distância do eixo? (a) , (b) , (c) , (d) , (e) ?
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão. Temos essas duas situações:
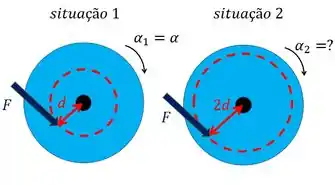
Temos o mesmo disco nas duas situações e a mesma força . Dizer que a força é tangencial, é o mesmo que dizer que ela é sempre perpendicular ao raio do disco, tudo bem? Então é perpendicular a e da nossa figura, sempre.
Ele diz que na situação 1, onde a força é aplicada a uma distância do eixo de rotação, o disco tem uma aceleração angular . E aí ele quer saber quando vale a aceleração angular se a distância entre a força e o centro do disco for .
Vamos descobrir essa aceleração!
Passo 2
Bem, a gente tá relacionando força e aceleração angular. Que equação faz isso? A segunda lei de Newton para rotação!
Onde é o momento de inércia do disco. Como o disco não muda, é o mesmo para as duas situações. Já é o torque resultante sobre o disco. Como há só uma força sobre ele, ela é a responsável pelo torque resultante. Na situação o torque vai ser dado por
Já que é a distância do ponto de aplicação da força até o eixo de rotação, e e são perpendiculares. Então a segunda lei de Newton para a situação 1 fica:
Logo achamos uma expressão para a , que é a aceleração angular da primeira situação.
Passo 3
Na segunda situação, o torque resultante é
Já que é a distância do ponto de aplicação da força até o eixo de rotação, e e são perpendiculares.
Aí a segunda lei de Newton agora fica
Lembrando que não muda, ok? Substituindo o torque:
Vimos no passo anterior que . Então a gente pode reescrever assim:
Ou seja, a alternativa b é a certinha 😊