Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 33.1 - Ex. 31
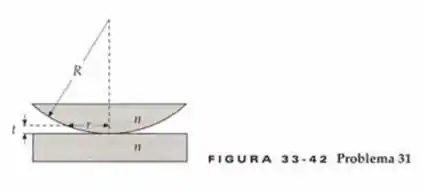
Um dispositivo para a obtenção de anéis de Newton consiste em uma lente plano-convexa de vidro com raio de curvatura que repousa sobre uma placa plana de vidro, como mostrado na Figura 33-42. O filme fino é de ar com espessura variável. O dispositivo é iluminado de cima pela luz de uma lâmpada de sódio com comprimento de onda de . O padrão é observado na luz refletida.
Mostre que para uma espessura a condição para um anel de interferência brilhante (construtiva) é , onde
Mostre que, para , o raio de uma franja está relacionado a por .
Para um raio de curvatura de e uma lente de de diâmetro, quantas franjas brilhantes você veria na luz refletida?
Qual seria o diâmetro da sexta franja brilhante?
Se o vidro usado no dispositivo tem índice de refração e o ar for substituído por água entre as duas partes de vidro, explique qualitativamente as variações que ocorrerão no padrão de franjas brilhantes.
Passo 1
E aí bonit@s, como vocês estão?
Se liguem só na estratégia que vamos utilizar pra resolver esse problema: Este arranjo é essencialmente idêntico a uma configuração de ″ filme fino ″, exceto que o ″ filme ″ é ar. Uma mudança de fase de ocorre no topo da placa de vidro plana. Podemos usar a condição para interferência construtiva para derivar o resultado dado em e usar a geometria da lente na placa para obter o resultado dado em Podemos então usar esses resultados nas partes restantes do problema. Da condição de interferência construtiva nós temos que
Resolvendo para encontramos
Passo 2
Da geometria do nosso problema esquematizada na figura nós temos que
Quando temos podemos neglicencia-lo de modo a obter
Passo 3
Utilizando a equação elevada ao quadrado e substituindo em vamos encontrar
Substituindo os valores numéricos vamos encontrar
Precisaremos de aproximadamente 68 franjas brilhantes.
Passo 4
Continuando nosso processo temos que o diâmetro da franja é
Sendo assim, substituindo os valores numéricos vamos obter
Passo 5
Por fim, temos que o comprimento de onda da luz no filme torna-se . A separação entre as franjas é reduzida (as franjas ficariam mais espaçadas) e o número de franjas que serão vistas é aumentado por um fator de 1,33. Pronto, resolvemos nosso problema.
Resposta
o comprimento de onda da luz no filme torna-se . A separação entre as franjas é reduzida (as franjas ficariam mais espaçadas) e o número de franjas que serão vistas é aumentado por um fator de 1,33