Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 31.1 - Ex. 67

O sódio tem estados excitados 2,11   e V ,   3,20 e V   e   4,35   e V acima do estado fundamental. Considere que os átomos do gás estejam todos no estado fundamental antes da irradiação.

a Qual é o máximo comprimento de onda da radiação que resultará da fluorescência de ressonância? Qual é o comprimento de onda da radiação fluorescente?

b Qual é o comprimento de onda que resultará da excitação do estado 4,35   e V acima do estado fundamental? Se o estado é excitado, quais são os possíveis comprimentos de onda da fluorescência ressonante que poderiam ser observados?

Passo 1

E aí bonit@s, como vocês estão?

Se liguem só na estratégia que adotaremos para essa questão: Como o comprimento de onda está relacionado à energia de um fóton por λ = h c / Δ E , comprimentos de onda mais longos correspondem a diferenças de energia menores. O estado fundamental e os três níveis de energia excitados podem ser ilustrados no seguinte esquemático

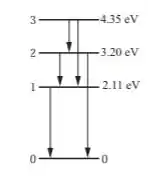
O comprimento de onda máximo de radiação que resultará na fluorescência de ressonância corresponde a uma excitação para o nível de 3,20   e V seguido por decaimentos para o nível de 2,11   e V e o estado fundamental, assim temos

λ m á x = 1240   e V ⋅ n m 3,20   e V = 388   n m

Os comprimentos de onda de fluorescência são

λ 2 → 1 = 1240   e V ⋅ n m 3,20   e V - 2,11   e V = 1140   n m

E

λ 1 → 0 = 1240   e V ⋅ n m 2,11   e V - 0 = 588   n m

Passo 2

Para a excitação teremos

λ 0 → 3 = 1240   e V ⋅ n m 4,35   e V = 285   n m     f o r a   d o   e s p e c t r o   v i s í v e l

Dessa forma, os possíveis comprimentos de onda para fluorescência serão dados por

λ 3 → 2 = 1240   e V ⋅ n m 4,35   e V - 3,20   e V = 1080   n m     f o r a   d o   e s p e c t r o   v i s í v e l

λ 2 → 1 = 1240   e V ⋅ n m 3,20   e V - 2,11   e V = 1140   n m     f o r a   d o   e s p e c t r o   v i s í v e l

λ 1 → 0 = 1240   e V ⋅ n m 2,11 e V - 0 = 588   n m    

λ 3 → 1 = 1240   e V ⋅ n m 4,35   e V - 2,11   e V = 554   n m    

λ 2 → 0 = 1240   e V ⋅ n m 3,20   e V - 0 = 388   n m     f o r a   d o   e s p e c t r o   v i s í v e l

Pronto, está resolvido nosso problema.

Resposta

a   λ m á x = 388   n m ,   λ 2 → 1 = 1140   n m   e   λ 1 → 0 = 588   n m    

b   λ 0 → 3 = 285   n m   ,     λ 3 → 2 = 1080   n m   ,     λ 2 → 1 = 1140   n m  

λ 1 → 0 = 588   n m   ,     λ 3 → 1 = 554   n m ,     λ 2 → 0 = 388   n m     f o r a   d o   e s p e c t r o   v i s í v e l

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

38.44. O comprimento de onda visível mais curto é aproximadamente igual a 400 nm. Qual é a temperatura de um corpo negro ideal cuja emitância espectral apresente um pico nesse comprimento de onda?
38.44. O comprimento de onda visível mais curto é aproximadamente igual a 400 nm. Qual é a temperatura de um corpo negro ideal cuja emitância espectral apresente um pico nesse comprimento de onda?
38.46. Duas estrelas, ambas se comportando como corpos negros, irradiam a mesma energia total por segundo. A mais fria delas tem uma temperatura de superfície T e seu diâmetro é 3,0 vezes maior que o
38.49. Mostre que, para valores grandes de λ , a distribuição de Planck, dada pela Equação (38.32), concorda com a distribuição de Rayleigh, dada pela equação (38.31)
38.42. Determine λ m , o comprimento de onda do pico da distribuição de Planck, e a frequência f correspondente nas seguintes temperaturas: a) 3,0K; b) 300 K; c) 3000 K.