Enunciado
Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 3.Problemas - Ex. 6
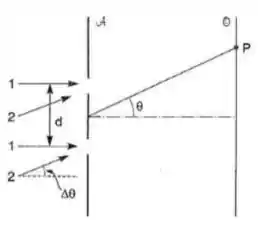
Considere o experimento de Young com um feixe incidente 1 perpendicular ao anteparo e um ponto na direção do anteparo de observação , onde a interferência é construtiva. Se agora acrescentarmos outro feixe incidente 2 que forma um ângulo com o feixe 1, e se formos aumentando , chegarmos a uma situação onde a interferência em é destrutiva para o feixe 2, ou seja, os mínimos de 2 caem sobre os máximos de 1 e, se os dois feixes tem a mesma intensidade (e frequência), as franjas de interferência desaparecem. Mostre que isso acontece para , onde é a separação das aberturas. Isso permite medir . Relacione esse resultado com o interferômetro estelas de Michelson (Seç 3.6).
Passo 1
Beleza, vamos começar pensando no experimento de Young SEM o segundo feixe. Sabemos que quando os dois feixes 1 (que são os paralelos com a horizontal) passam pelas duas aberturas, respeitando o princípio de Huygens, as frentes de onda secundárias vão passar pelos caminhos e até o ponto P. E a equação de diferença de caminhos é:
E as faixas claras e escuras que se formam no anteparo quando a luz bate respeitam a seguinte equação para o caso de interferência destrutiva (que é o que estamos interessados):
Podemos juntar as duas equações:
Sendo que é o número de franjas formadas a partir do centro do anteparo alvo.
A separação entre dois mínimos (e máximos) fica, se considerarmos que a variação de é muito pequena, podemos fazer :
Para dois próximos um do outro (vamos pegar e como exemplo:
Sobra:
Que é a equação que está no livro, isso é o mesmo que pegarmos dois pontos que marcam exatamente as bordas de uma das franjas, e calcularmos a diferença angular entre esses dois pontos.
Passo 2
Agora para o nosso caso, em que existe um novo feixe, que chamaremos de 2, passando pela fenda junto com o feixe 1 e causando uma interferência destrutiva para um ângulo . Esse feixe faz com que TODAS as franjas sumam. O que significa que a gente precisa adaptar a equação para esse caso, já que agora o número de franjas não depende mais do ângulo .
Então a gente tira o da equação:
Ou seja, para qualquer diferença de caminhos entre os feixes resultantes (que é o feixe final depois que os dois feixes 1 e 2 se juntam na abertura), o valor sempre depende da metade do comprimento de onda
Passo 3
Agora a gente passa o dividindo para o lado direito:
E para situações em que é pequeno:
A equação se torna:
Como não existem franjas, a gente não pode pegar dois pontos que marcam exatamente a mudança de franja clara para escura, e por isso não se trata de mas sim um valor de único.
Passo 4
No caso do experimento de Michelson acontece exatamente isso, a luz proveniente de uma estrela pode ser usada para produzir as franjas de Young e dependendo do ângulo formado entre os raios incidentes, essas franjas param de se formar. Quando isso acontece é possível estimar o diâmetro da estrela.