Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.3 - Ex. 27
Dois blocos, com e de peso, estão ligados por uma corda sem massa e deslizam para baixo em um plano inclinado de . O coeficiente de atrito cinético entre o bloco mais leve e o plano é e o coeficiente de atrito cinético entre o bloco mais pesado e o plano é . Supondo que o bloco mais leve desce na frente, determine (a) o módulo da aceleração dos blocos e (b) a tensão da corda.
Passo 1
Belezera pessoal, vamos iniciar esta questão fazendo o diagrama do corpo livre de cada bloco, primeiro para o bloco mais leve, o bloco , dado como:
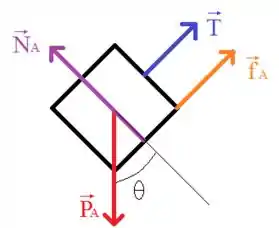
Agora para o bloco :
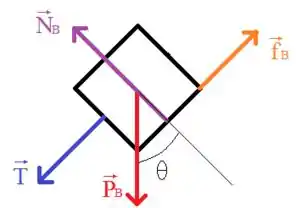
A partir daí podemos visualizar melhor como as forças estão atuando nos blocos e, então, podemos aplicar a segunda lei de Newton para cada eixo dos blocos. Vamos iniciar escrevendo as equações do bloco mais leve, no eixo da rampa, temos:
Já no eixo perpendicular a rampa, obtemos:
De maneira análoga para o bloco mais pesado, bloco no eixo da rampa:
Enquanto no eixo perpendicular a rampa:
Lembrando que, como os blocos estão em movimento, a força de atrito que age sobre os bloco é a força de atrito cinético que pode ser calculado usando a seguinte relação:
Passo 2
Vamos começar a resolver este problema definindo a força de atrito cinético do bloco mais leve, lembrando que:
Substituindo esta expressão na equação da força de atrito:
De maneira análoga, para o bloco mais pesado:
Logo:
Passo 3
Agora, vamos isolar o na equação do bloco , no eixo da rampa:
Logo;
E como , obtemos que:
Passo 4
Agora se a gente pegar a equação para o bloco , no eixo da rampa, temos:
Substituindo a tração que encontramos, vemos que:
E lembrando também que :
Isolando o :
E a massa, podemos lembrar que se dividirmos a força pessoa pela gravidade , obtemos a massa de cada bloco, tal que:
Substituindo os valores dados no enunciado:
Passo 5
Agora, para determinar a tensão na corda, substituímos os valores na equação:
Logo:
Resposta
- ;
- .