20. Um popular passatempo consiste em ver quem consegue empurrar um objeto para mais perto da borda de uma mesa sem que ele caia para fora. Você empurra o objeto de e o libera a da borda da mesa. Infelizmente, seu empurrão foi um pouco forte demais. O objeto desliza através da mesa, sai voando pela borda, cai até o chão e aterrissa a da borda da mesa. Se o coeficiente de atrito cinético vale , qual era o valor da velocidade do objeto quando você o soltou?
Passo 1
Opa! Aqui vamos nós de novo!
Olha só! Primeiramente vamos fazer um desenhozinho pra mostrar o que vai acontecer em nosso problema. Aqui está...
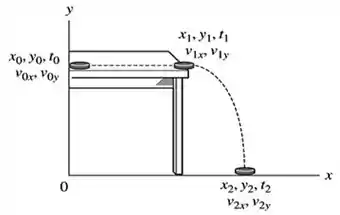
Dessa figura, sabemos os seguintes dados:
E o objetivo aqui, é encontrar . Por isso, comecemos de vez, fazendo o diagrama de corpo livre para o nosso objeto...
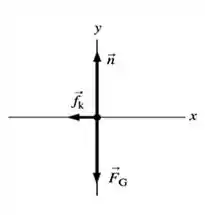
Essa força é a responsável por desacelerar o disco durante o seu percurso na mesa. O disco incialmente tem velocidade e é lançado sobre a mesa, sendo desacelerado até sair da mesa, numa velocidade horizontal .
Entendeu! Se sim, tá na cara que o melhor jeito de se achar é através da equação abaixo...
Passo 2
Sendo assim, vamos usar a segunda lei de Newton pra descobrir o valor de ...
Primeiro, o somatório das forças na direção vertical. Isto, pra quando o disco estiver na mesa.
Bom! Agora ficou fácil! A força de atrito é o produto da normal pelo coeficiente de atrito e é a única força agindo na horizontal, com sinal negativo, é claro, porque se opõe ao movimento... Temos então, que...
Passo 3
Em seguida, bora partir por eixo e usar a equação abaixo pra descobrir o tempo que o objeto leva para chegar até o chão, quando sai da mesa;
Não podemos esquecer que o objeto também vai ter um movimento horizontal. Afinal, nesse tipo de lançamento temos dois movimentos, o vertical e o horizontal. Logo, usemos a equação abaixo...
Passo 4
Obtido os valores que precisávamos... Agora sim, vamos obter o valor de pela equação abaixo...
E pronto! Finalizamos aqui! Essa é a velocidade do objeto quando foi solto!