Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.3 - Ex. 32

Uma caixa de brinquedos e seu conteúdo têm um peso total de 180   N . O coeficiente de atrito estático entre a caixa de brinquedos e o piso é 0,42 . A criança da Fig. 6-35 tenta arrastar a caixa puxando-a por uma corda. (a) Se θ = 42 ° , qual é o módulo da força F → que a criança deve fazer sobre a corda para que a caixa esteja na iminência de se mover? (b) Escreva uma expressão para o menor valor do módulo de F → necessário para que a caixa se mova em função do ângulo θ . Determine (c) o valor de θ para o qual F é mínimo e (d) o valor desse módulo mínimo.

Passo 1

Vamos começar esta questão fazendo o DCL da caixa de brinquedos:

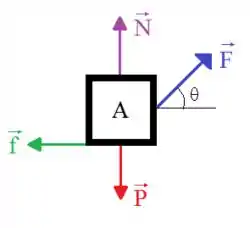
A partir dessa ilustração já somos capazes de visualizar as forças que atuam na caixa e suas respectivas direções e sentidos. Assim, podemos aplicar a segunda lei de Newton para cada eixo, lembrando que estamos considerando a caixa na iminência do movimento, ou seja, a aceleração da caixa é nula e a força de atrito estático é máxima:

e i x o   x :       F cos ⁡ θ - f s m á x = 0       e q . 1

e i x o   y :       F sin ⁡ θ + N - P = 0       e q . 2

Lembrando que podemos determinar o módulo da força de atrito estático máximo usando a seguinte relação:

f s m á x = μ s N       e q . 3

Passo 2

Para determinar o módulo de F → para que esteja na iminência do movimento, vamos iniciar determinando o valor de f s m á x → usando a e q . 3 :

f s m á x = μ s N

Para determinar o valor da normal, vamos isolá-lo na e q . 2 :

N = P - F sin ⁡ θ

Substituindo este valor na e q . 3 :

f s m á x = μ s P - μ s F sin ⁡ θ     e q . 4

Passo 3

Usando a e q . 4 na e q . 1 :

F cos ⁡ θ - μ s P + μ s F sin ⁡ θ = 0

F cos ⁡ θ + μ s sin ⁡ θ - μ s P = 0

Isolando F :

F = μ s P cos ⁡ θ + μ s sin ⁡ θ       e q . 5

Substituindo os valores conhecidos:

F = 0,42 × 180 cos ⁡ 42 ° + 0,42 × sin ⁡ 42 ° = 73,8   N

Portanto, a força que o menino deve aplicar para deixar a caixa na iminência do movimento é 73,8   N .

Passo 4

A expressão para a força mínima que o menino deve fazer em função do ângulo θ já foi determinado no passo anterior, tendo em vista que a mínima força para deixar a caixa em movimento é aquela que a força de atrito estático máximo é alcançado. Assim, vamos substituir os dados na e q . 5 deixando apenas em função de θ :

F θ = 0,42 × 180 cos ⁡ θ + 0,42 × sin ⁡ θ       e q . 6

Passo 5

Para encontrar o máximo ou mínimo de qualquer função, podemos usar o artifício da derivada, então podemos derivar a e q . 6 e analisar os pontos críticos dessa derivada. Assim:

F ' θ = - - sin ⁡ θ + 0,42 × cos ⁡ θ × 75,6 cos ⁡ θ + 0,42 × sin ⁡ θ 2

F ' θ = 75,6 × sin ⁡ θ - 0,42 × cos ⁡ θ cos ⁡ θ + 0,42 × sin ⁡ θ 2

Neste caso, somente a expressão que está entre parênteses no numerador pode dar zero e zerar toda a nossa função. Assim, para determinarmos o θ que a força é mínima, basta determinar o θ que zera essa expressão:

sin ⁡ θ - 0,42 × cos ⁡ θ = 0

sin ⁡ θ = 0,42 × cos ⁡ θ

tan ⁡ θ = 0,42

Isolando o θ :

θ = tan - 1 ⁡ 0,42 = 22,8 °

Passo 6

Para determinar o módulo de F → mínimo, substituímos este valor de θ = 22,8 ° na e q . 6 , assim:

F m í n = 0,42 × 180 cos ⁡ 22,8 ° + 0,42 × sin ⁡ 22,8 ° = 69,7   N

Resposta

  1. F = 73,8   N ;
  2. F θ = 0,42 × 180 cos ⁡ θ + 0,42 × sin ⁡ θ ;
  3. θ = 22,8 ° ;
  4. F m í n = 69,7   N .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bola de beisebol é atirada verticalmente para cima. A força de arraste é proporcional a v 2 . Em termos de g, qual é o componente y da aceleração quando a velocidade é igual à metade da velocidade
Uma caixa de ferramentas de 45,0 k g está em repouso sobre um piso horizontal. Você exerce sobre ela uma força de puxar horizontal que aumenta gradualmente e observa que a caixa sócomeça a se mover qu
Como indicado na Figura 5.54 , o bloco A (massa de 2,25k g ) está em repouso sobre o topo de uma mesa. Ele é ligado a um bloco B (massa de 1,30k g ) por uma corda horizontal que passa sobre uma polia
Duas caixas estão ligadas por uma corda sobre uma superfície horizontal (Figura 5.55 ). A caixa A possui massa m A e a caixa B possui massa m B . O coeficiente de atrito cinético entre cada caixa e a
Os blocos A, B e C são dispostos como indicado na Figura 5.56, e ligados por cordas de massas desprezíveis. O peso de A é de 25,0 N e o peso de B também é de 25,0 N. O coeficiente deatrito cinético en