Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 68
Dois blocos estão em contato sobre uma superfície horizontal sem atrito. Os blocos são acelerados por uma força única horizontal aplicada a um deles (Figura 4-52). Encontre a aceleração e a força de contato do bloco 1 sobre o bloco 2 (a) em termos de F, e , e (b) para os valores específicos e
Passo 1
a) Oi pessoal, tudo bem? Vamos analisar essa questão. Ele quer a aceleração dos blocos, que é a mesma, porque eles se movem coladinhos. E quer uma expressão para a força de contato do bloco 1 sobre o bloco 2, que vamos chamar de .
Pela terceira lei de Newton, se o bloco 1 exerce uma força no bloco 2, o bloco 2 vai exercer uma força de mesmo módulo e sentido oposto no bloco 1, que vamos chamar de .
O diagrama de corpo livre, para a situação descrita, está exposto abaixo:
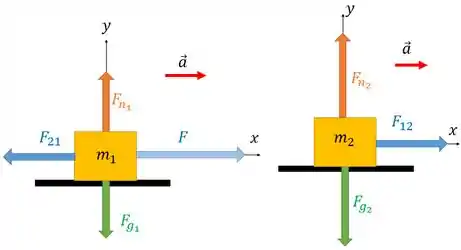
A força atua na objeto 1. E cada bloco tem força peso apontando para baixo por ter cada um sua massa. E ambos tem força normal por estarem em contato com uma superfície.
A ideia aqui é a gente aplicar a segunda lei de Newton em cada bloco para descobrir a aceleração dos blocos e descobrir .
Passo 2
Como a aceleração e estão na direção , vamos aplicar a lei de Newton para os dois blocos nessa direção.
Aplicando a segunda lei de Newton na caixa de massa :
Temos aqui no sentido positivo de , logo ele aparece positivo, e o contrário acontece com :
Aplicando a segunda lei de Newton na caixa de massa , temos:
Aqui a única força na direção é , que é positiva:
Como pela terceira lei de Newton as forças de contato entre os blocos tem a mesma magnetude , podemos substituir a equação em :
Percebe que a gente pode colocar em evidência aqui porque ela é a mesma para os dois blocos. E a gente quer a expressão dela, lembra? Então vamos isolar essa bonita:
Queremos também a expressão de . Então vamos substituir essa aceleração que a gente achou em :
Passo 3
b) Agora ele quer que a gente use nossas expressões para achar os valores de e a partir dos dados que ele dá. A gente viu que a força é dada por
Substituindo os dados:
E a aceleração é dada por
Substituindo os dados: