Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 52

Para o sistema das Figuras 4-41a, 4-41b e 4-41c, encontre as massas e as tensões desconhecidas.

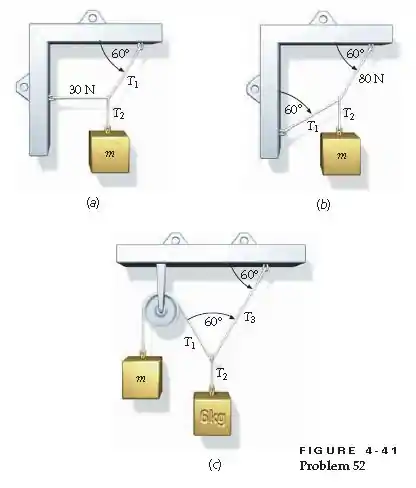
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Aqui estão os 3 diagramas de corpo livre para os itens do enunciado:

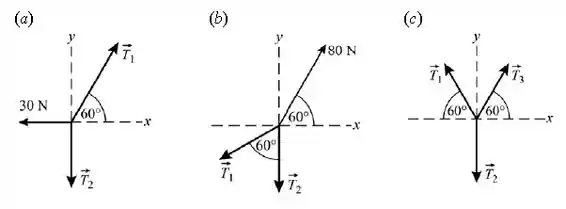
Por definição, temos que:

∑ F x = m a x

∑ F y = m a y

Temos que, para que os sistemas se encontrem em repouso, ∑ F x e ∑ F y devem ser iguais a zero.

Para o item (a), temos:

∑ F x = T 1 cos ⁡ 60 ° - 30 = 0

∑ F y = T 1 sin ⁡ 60 ° - T 2 = 0

Resolvendo, temos que:

T 1 = 30 cos ⁡ 60 °

T 1 = 60   N

T 2 = T 1 sin ⁡ 60 ° = 60 ⋅ sin ⁡ 60 °

T 2 = 51,96   N

Como T 2 é o peso do objeto, podemos encontrar sua massa. Temos que:

T 2 = m g

m = T 2 g

m = 51,96 9,81

m = 5,3   k g

Passo 2

Para o item (b), temos:

∑ F x = 80 cos ⁡ 60 ° - T 1 sin ⁡ 60 ° = 0

∑ F y = 80 sin ⁡ 60 ° - T 2 - T 1 cos ⁡ 60 ° = 0

Resolvendo, temos que:

T 1 = 80 cos ⁡ 60 ° sin ⁡ 60 °

T 1 = 46,19   N

T 2 = 80 sin ⁡ 60 ° - 46,19 cos ⁡ 60 °

T 2 = 46,19   N

Como T 2 é o peso do objeto, podemos encontrar sua massa. Temos que:

T 2 = m g

m = T 2 g

m = 46,19 9,81

m = 4,7   k g

Passo 3

Para o item (c), temos:

∑ F x = - T 1 cos ⁡ 60 ° + T 3 cos ⁡ 60 ° = 0

∑ F y = T 1 sen ⁡ 60 ° + T 3 sen ⁡ 60 ° - T 2 = 0

Esse M = 6 k g , não é a massa que queremos descobrir, mas sim a massa de 6kg representada no desenho da questão.

Da primeira equação tiramos que

- T 1 cos ⁡ 60 ° + T 3 cos ⁡ 60 ° = 0 → - T 1 + T 3 = 0

T 1 = T 3

Resolvendo, temos que:

T 1 = T 3 = T 2 2 sin ⁡ 60 ° = T 2 2 3 2 = T 2 3

A tensão T 2 é igual ao peso da massa de 6kg

T 2 = M g = 6 ⋅ 9,8 1 = 58,8 6   N

Assim

T 1 = T 3 = T 2 3 = 58,8 6 3 = 33,98 N

Como T 1 é o peso do objeto que queremos, então

T 1 = m g

m = T 1 g = 33,98 9,8 1 = 3,4 6   k g

Resposta

a ) T 1 = 60   N

T 2 = 51,96   N

m = 5,3   k g

b ) T 1 = 46,19   N

T 2 = 46,19   N

m = 4,7   k g

c ) T 1 = T 3 ≅ 34   N

T 2 = 58,8 6   N

m ≅ 3,5   k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um arqueólogo aventureiro passa de um rochedo para outro deslocando-se lentamente com as mãos por meio de uma corda esticada entre os rochedos. Ele para e fica em repouso no meio da corda (Figura 5.42
Uma bola grande de um guindaste de demolição é mantida em equilíbrio por dois cabos de aço leves (Figura 5.43 ). Se a massa m da bola for igual a 4090k g , qual é a) a tensão T B no cabo que faz um ân
Ache a tensão em cada corda na Figura 5.44 , sabendo que o peso suspenso é p .
Em quase todos os problemas deste livro, as massas dos cabos, cordas e fios são tão pequenas em comparação com os outros corpos que podemos desprezá-las. Porém, quando a corda é o único objeto do prob
Um bloco de massa M é amarrado na extremidade inferior de uma corda de massa m e comprimento L . Uma força F → constante é aplicada de baixo para cima na extremidade superior da corda, fazendo com que