Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 14.1 - Ex. 75
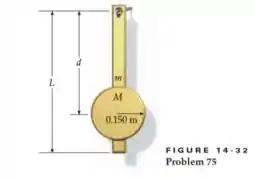
A Figura 14-32 mostra o pêndulo de um relógio na casa da sua avó. A haste uniforme de comprimento L = 2,00 m tem uma massa m = 0,800 kg. Anexado à haste está um disco uniforme de massa M = 1,20 kg e raio de 0,150 m. O relógio é construído para manter o tempo perfeito se o período do pêndulo for exatamente de 3,50 s. (a) Qual deve ser a distância d para que o período deste pêndulo seja de 2,50 s? (b) Suponha que o relógio atrase 5,00 min por dia. Para garantir que sua avó não se atrase para as festas de acolchoados, decida ajustar o relógio novamente para o período adequado. A que distância e em que direção você deve mover o disco para garantir que o relógio mantenha o tempo perfeito?
Passo 1
a) Percebe que temos um pêndulo estranho formado por uma haste e um disco, então ele é o que chamamos de um pêndulo físico. E queremos para que o período que antes era de seja de .
Podemos usar a equação do período de um pêndulo físico para resolvermos a letra (a):
Vamos ver cada variável dessa. Nesse caso, é a distância entre o eixo de rotação e o centro de massa do nosso pêndulo. Se a gente considerar que a origem do nosso sistema está no próprio eixo de rotação, vai ser igual ao módulo da posição do CM, então:
Por se tratar de uma altura, estou chamando a posição do centro de massa de .
Vamos achar esse . Precisamos escrever a posição do centro de massa em termos da distância (porque ela é uma incógnita). E para isso, usaremos a relação para achar o CM de uma figura composta:
Para saber a posição do centro de massa de cada um desses objetos, têm uma figura esperta aqui, olha só:
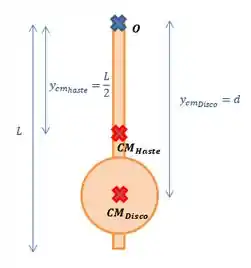
Imagina que o eixo está para baixo e o eixo está para a direita. A origem deles é no eixo de rotação (onde o pêndulo está pendurado). O CM da barra fica em sua metade e o disco em seu centro.
Sendo assim, teremos:
Passo 2
Agora vamos ver . Esse é o momento de inércia da nossa peça toda, em relação ao eixo de rotação.
Esse pêndulo físico é composto por dois objetos, uma haste delgada e um disco.
Para calcular o seu momento de inércia, teremos que ele será a soma dos dois momentos de inércia, em relação ao eixo de rotação
Vamos começar calculando o momento de inércia do disco. Sabemos que o momento de inércia do disco com relação ao seu centro de massa é:
Onde é a massa do disco e é o raio do disco.
No entanto, o eixo de rotação não passa pelo centro de massa do disco, o eixo é o eixo do relógio que está a uma distância do centro de massa do disco:
Por conta disso, precisaremos usar o teorema dos eixos paralelos, que nos dá o momento de inércia do disco com relação a esse eixo, que eu to chamando de eixo :
Onde é a distância entre os eixos, que no caso, é a própria distância que queremos encontrar.
Com isso, teremos para o disco:
Agora para a haste, sabemos que o momento de inércia de uma barra fina homogênea, para um eixo que passe no seu centro de massa, é:
Onde é a massa da barra e é o seu comprimento.
No entanto, o eixo de rotação não passa no centro de massa da barra e sim lá em cima:
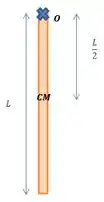
E por isso, vamos precisar do teorema dos eixos paralelos aqui também.
Aonde aqui a distância entre os eixos será igual a metade do comprimento da barra
E por fim, teremos:
Agora, é só somar esses dois:
Substituindo valores numéricos para todas as grandezas na equação do momento de inercia:
Passo 3
Vamos voltar na nossa expressão para o período:
Podemos usa-la para achar para que como ele pede. é massa total do pêndulo
Temos o valor e a expressão de todas essas variáveis. Vamos isolar e que dependem de :
Substituindo as expressões que achamos e os dados do enunciado, lembrando que
Isolando e resolvendo:
Ufa! Prontinho!
Passo 4
b) Cara, o relógio foi projetado para medir o tempo perfeitamente se
Então se ele está medindo o tempo errado, significa que esse período está errado. E isso é causado pela posição errada de .
Ele diz que o relógio se atrasa 5 minutos a cada dia. Então, num dia começando 00:00h, 24 horas depois, ele não vai estar em 00:00h, mas em 23:55h.
Como um dia tem 1440 minutos, quer dizer que com valor de atual, ele percorre a distância que representa 1435 minutos.
Imagina que dentro dos 1440 minutos ele deveria percorrer os do relógio (dar aquela volta completa). Mas em vez disso, ele deixa de percorrer o equivalente a , que pode ser escrito em como uma fração de assim:
Que é a fração que representa 5 minutos no relógio. Então, na verdade, ele percorre
Mas pensa comigo: o ponteiro sempre mantém a mesma velocidade né? Então quer dizer que essa distância percorrida vai ser proporcional ao tempo. Assim, a gente pode fazer uma regra de 3 entre o período do pêndulo que faz o ponteiro se mover e a distância percorrida por ele.
Temos que no período , que o pêndulo tem antes de arrumar , ele percorre .
Mas no período depois da correção , ele vai percorrer . Então temos algo assim
Multiplicando cruzado
Isolando e resolvendo:
Descobrimos o período atual do relógio que precisa ser arrumado.
Passo 5
Agora precisamos descobrir para esse período errado e para o correto e fazer a diferença entre os dois para saber o quanto a gente precisa mover o disco.
Vamos usar a equação do passo 3:
Lembrando que
Para :
Para :
E fazemos a diferença entre os dois valores para sabermos o quanto precisamos subir o pendulo para que o relógio volte a funcionar de acordo com a maneira como foi construído:
Precisamos mover então nosso disco de para baixo (aumentando )