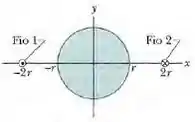
Dois fios, paralelos ao eixo e separados por uma distância de , conuem correntes iguais em sentidos opostos, como mostra a figura 32-28. Um cilindro circular de raio e comprimento tem o eixo central sobre o eixo , a meio caminho entre os fios. Com base na lei de Gauss, escreva uma expressão para o fluxo magnético através da metade da superfície lateral do cilindro que está acima do eixo .

Já para campos magnético, que são contínuos e formam curvas fechadas, a situação é um pouco diferente!

O que acontece aqui é que as linhas de campo não começam e terminam em qualquer ponto, conforme a figura (a) a seguir.

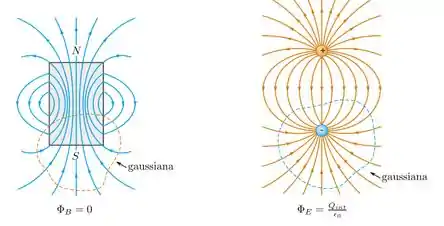
Podemos observar que qualquer superfície fechada, tal como a linha tracejada na figura da esquerda acima, o número de linhas que entram é igual ao número de linhas que saem, então o fluxo magnético é zero! No contrário, para uma superfície fechada ao redor de uma carga de dipolo elétrico, conforme a figura da direita, o fluxo elétrico total não é zero.

Assim,

Tranquilo? 😇

Logo, usando a lei de Gauss para campos magnéticos, o fluxo através da metade da superfície lateral do cilindro que está acima do eixo é igual ao fluxo através da parte do plano que está no interior do cilindro.

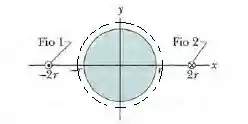
Assim,

E aí! entendeu tudo? Responde Aí! 😬