Exercícios de Equações de Maxwell - Lista de Exercícios Resolvida

Encontre a forma integral das equacões abaixo:

Usando a identidade vetorial:

Mostre que o campo magnético satisfaz a equação da onda.

O campo elétrico de uma onda eletromagnética no vácuo é dado por com

Onde , e são constante positivas. O valor máximo atingido pelo módulo do campo elétrico

1. Use a forma diferencial da lei de Gauss para determinar e em termos de .
2. Sabendo que o campo elétrico satisfaz a equação de onda tridimensional, determine a constante em termos da velocidade da luz no vácuo e ;
3. Use a forma diferencial da lei de Faraday para determinar o campo magnético associado ao campo elétrico dado em termos de , e da velocidade da luz no vácuo .

Use os operadores diferenciais e os teoremas da divergência e de stokes para passar as equacões de Maxwell abaixo para a forma diferencial.

A partir das equações de Maxwell no vácuo, encontre a equação diferencial de onda para o campo elétrico .

Use os operadores diferenciais e os teoremas de Gauss e Stokes para passar as leis de Maxwell abaixo para a forma diferencial. (Qint ≡ Qsaldo)

(a ) onde e

(b )

O teorema de Poynting é representado pela equação

a qual descreve o que ocorre com um campo eletromagnético em um volume V do espaço, limitado por uma superfície fechada S de área A, sendo ambos (V e S) regiões simplesmente conexas. O símbolo UEM designa a energia do campo eletromagnético no volume V. O vetor de Poynting é S e o vetor J designa a densidade de corrente elétrica em um ponto no interior do volume V.

(a ) Dê o significado convencional dos termos da equação acima.

A lei de Gauss para o magnetismo nos diz:

A existência de uma carga resultante em qualquer volume.

Que é nula a integral de linha de um campo magnético em qualquer percurso fechado.

O campo magnético gerado por um elemento de corrente.

A inexistência de monopolos magnéticos.

As cargas devem se mover para produzir campo magnético.

Um campo magnético não estacionário atravessa uma espira de área . A corrente induzida na espira é associada a um campo eletrostático. Verdadeiro ou falso?

Considerando-se os fenômenos eletromagnéticos, aqueles que ocorrem envolvendo os campos magnéticos e elétricos coexistindo no mesmo fenômeno, NÃO podemos afirmar:

1. A lei de Faraday preconiza que quando um campo magnético varia, há o surgimento de um campo elétrico.
2. As equações de Maxwell correlacionam as leis de Ampère, Faraday, Lenz e Gauss em um único grupo de equações.
3. As equações de Maxwell não fornecem a velocidade das ondas eletromagnéticas no vácuo, que demonstrou-se posteriormente serem variáveis.
4. Os fenômenos elétricos e magnéticos estão correlacionados através de uma teoria chamada eletromagnetismo.
5. Obtém-se experimentalmente que quando um campo elétrico varia, gera um campo magnético

A partir das equações de Maxwell no vácuo, encontre a equação diferencial de onda para o campo elétrico .

A lei de conservação da carga para sistemas abertos (equação da continuidade) é

representada pela equação

Dê o significado convencional dos termos dessa equação.

Use os operadores diferenciais e os teoremas de Gauss e Stokes para passar as leis de Maxwell abaixo para a forma diferencial. (Qint ≡ Qsaldo)

(a ) onde e

(b )

Responda corretamente e justifique suas opções:

a-( ) Não é nulo o divergente do campo magnético gerado por uma corrente elétrica dependente do tempo existente no fio que, enrolado, constitui a bobina.

b-( ) É nulo o rotacional do campo magnético em um ponto do espaço vazio entre as placas de um capacitor que está sendo carregado por uma fonte de tensão constante.

Parte :

Considere um sistema cujos vetores campo elétrico e magnético são dados por   e  , respectivamente, onde são constantes e denotam coordenadas cartesianas. Usando as equações de Maxwell, determine:

1. A densidade de carga do sistema.
2. O vetor densidade de corrente  do sistema.

No século XIX, um cientista inglês desenvolveu um grupo de equações que são consideradas a base da teoria eletromagnética, pois representou a correlação das leis de Ampère, Faraday, Lenz e Gauss em um único grupo de equações (quatro na realidade). Como é denominado esse grupo de equações?

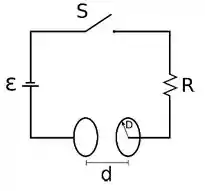
Um circuito é formado por uma chave , uma fonte ideal , um resistor de resistência e um capacitor com constante dielétrica . O capacitor é formado por duas placas circulares e paralelas com raio e separadas por uma distância . No instante a chave é fechada. Suponha que o campo elétrico entre as placas é uniforme.

a) Calcule a corrente de deslocamento no capacitor.

b) Calcule a taxa de variação no tempo do campo elétrico, , no capacitor.

c) Qual é o módulo do campo magnético no interior do capacitor no instante a uma distância radial medida a partir do centro do capacitor.

Sobre as equações de Maxwell, é incorreto afirmar:

1. A direção e propagação da onda eletromagnética é dada pelo produto vetorial dos vetores campo elétrico e campo magnético
2. O vetor campo elétrico e o vetor campo magnético propagam-se a velocidade da luz
3. O vetor campo elétrico e o vetor campo magnético são perpendiculares entre si
4. As equações de Maxwell geraram equações de ondas (eletromagnéticas) para a propagação do campo elétrico e do campo magnético no vácuo
5. O vetor campo elétrico e o vetor campo magnético não estão em fase

O campo elétrico de uma onda eletromagnética no vácuo é dado por com

Onde , e são constante positivas. O valor máximo atingido pelo módulo do campo elétrico

1. Use a forma diferencial da lei de Gauss para determinar e em termos de .
2. Sabendo que o campo elétrico satisfaz a equação de onda tridimensional, determine a constante em termos da velocidade da luz no vácuo e ;
3. Use a forma diferencial da lei de Faraday para determinar o campo magnético associado ao campo elétrico dado em termos de , e da velocidade da luz no vácuo .

O campo elétrico de uma onda eletromagnética no vácuo é dado por com

Onde , , e são constantes positivas.

O valor máximo atingido pelo módulo do campo elétrico é .

1. Use a forma diferencial da lei de Gauss para determinar e em termos de .
2. Sabendo que o campo elétrico satisfaz a equação de onda tridimensional, determine a constante em termos da velocidade da luz no vácuo e .
3. Use a forma diferencial da lei de Faraday para determinar o campo magnético associado ao campo elétrico dado em termos de , e da velocidade da luz no vácuo .

Seja um campo elétrico propagando-se no vácuo tal que

(a) Mostre que este campo satisfaz à Lei de Gauss em sua forma diferencial.

(b) Aplique a Lei de Ampère em sua forma diferencial para encontrar a expressão

para o campo magnético.

(c) Mostre que obedece a equação de onda e com isso comprove que a velocidade

de propagação da luz é igual a .

Os valores experimentais da permissividade elétrica e permeabilidade magnética de um dado material valem e , respectivamente. Determine a velocidade de propagação de um feixe de luz no material.

(a)

(b)

(c)

(d)

(e)

O campo elétrico na região considerada na figura é dado por sendo uma constante positiva.

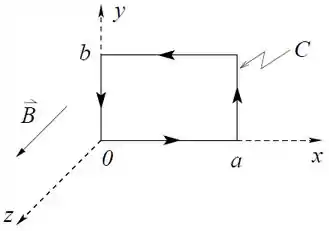
Calcule a densidade de carga na região.

Considere as afirmações abaixo e assinale a alternativa correta:

1. De acordo com a lei Ampère-Maxwell, durante o processo de carga de um capacitor de placas paralelas por uma corrente constante o campo elétrico entre as placas não é estacionário.
2. As linhas de campo magnético não nascem nem morrem nos ímãs, apenas os atravessam, ao contrário do que ocorre com os corpos condutores eletrizados que originam linhas de campo elétrico.
3. A concentração das linhas de força do campo elétrico ou das linhas de campo magnético indica, qualitativamente, onde a intensidade do respectivo campo é maior.

Escolha uma:

1. Somente as afirmativas e são verdadeiras;
2. Somente a afirmativa é verdadeira;
3. Todas as afirmativas são verdadeiras;
4. Somente as afirmativas e são verdadeiras
5. Somente as afirmativas e são verdadeiras.

Considere um sistema cujos vetores campo elétrico e magnético são dados e respectivamente, onde e são constantes e denotam coordenadas cartesianas e, denota a variável temporal. Usando as equações de Maxwell, determine o módulo da densidade de corrente do sistema para e .

Um capacitor está conectado a um resistor e a uma fonte de voltagem alternada como mostrado na figura. A fonte fornece uma fem dada por . As placas do capacitor são discos de raio . O ponto está entre duas placas, equidistante destas e a uma distância do centro do eixo de simetria. De acordo com a teoria eletromagnética, no ponto

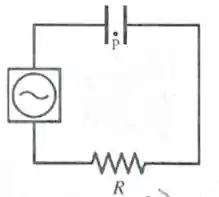
1. Não há campo magnético porque não existe carga se movendo entre as placas.
2. Existe um campo magnético constante.
3. Existe uma corrente de elétrons fluindo.
4. Existe um campo elétrico constante no tempo.
5. Existe um campo magnético variável no tempo.

Considere as informações sobre o vetor densidade de deslocamento, introduzida por J. C. Maxwell nas equações do eletromagnetismo. A sentença correta é:

(a) sua unidade física é (Àmpere por metro quadrado).

(b) é diferente de zero apenas em locais onde o campo elétrico é constante no tempo.

(c) é constituída por monopolos magnéticos em movimento.

(d) é proporcional ao fluxo do campo magnético sobre uma superfície fechada

2. Dos campos abaixo, quais campos elétrico e magnético satisfazem as equações de Maxwell?

Escolha uma:

(a) Nenhuma das alternativas

(b) e

(c) e

(d) e

(e) e

Um capacitor de placas circulares paralelas está sendo carregado. Calcule o raio das duas placas, sabendo que o raio das duas placas são iguais, a taxa de variação temporal do campo elétrico é igual a e que a intensidade do campo magnético gerado pela variação do campo elétrico é . Dados: a constante de permissividade elétrica no vácuo é e o coeficiente de permeabilidade magnética no vácuo é

Pode-se obter, a partir das equações de Maxwell, as equações que regem os campos

elétrico e magnético de uma onda em um meio condutor. A do campo elétrico é:

Admitindo o vetor intensidade do campo elétrico na forma

como solução da equação acima, obtém-se

evidenciando que o vetor de onda k é complexo.

(d ) Considere . Substitua esse k na função . Observando como fica essa função, escreva o significado de .

Considere as afirmações a seguir e marque a alternativa CORRETA.

1. Os campos elétrico e magnético são sempre perpendiculares entre si no vácuo.
2. As ondas eletromagnéticas podem ser justificadas com as equações de Maxwell sem o termo dado pela corrente de deslocamento.
3. Uma onda eletromagnética estacionária dentro de uma cavidade condutora possui o CAMPO MAGNÉTICO identicamente nulo nas paredes da cavidade.

1. Todas estão incorretas.
2. Todas estão corretas.
3. Apenas está correta.
4. Apenas está correta.
5. Apenas está correta.
6. Apenas e estão corretas.
7. Apenas e estão corretas.