Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 23.7 - Ex. 29
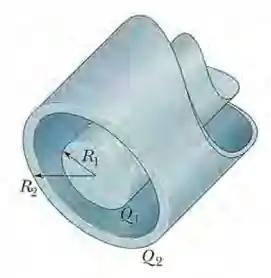
A Fig. 23-38 é uma seção de uma barra condutora de raio e comprimento no interior de uma casca coaxial, de paredes finas, de raio e mesmo comprimento . A carga da barra é ; a carga da casca é . Determine (a) o módulo e (b) a direção (para dentro ou para fora) do campo elétrico a uma distância radial . Determine (c) e (d) a direção do campo elétrico para . Determine a carga (e) na superfície interna e (f) na superfície externa da casca.
Passo 1
(a) Usando novamente a Lei de Gauss, temos, para uma superfície cilíndrica de raio que envolve a casca cilíndrica maior da figura:
Então:
Passo 2
(b) Como o sinal encontrado anteriormente é negativo, então, esse campo elétrico que encontramos está direcionado para o eixo central.
Passo 3
(c) Quando a gente considera uma superfície gaussiana com raio a história muda, pois, nesse caso, o raio da superfície é menor que o da casca esférica mais externa. Então, na Lei de Gaus a carga interna à superfície gaussiana considerada somente contabiliza a carga da barra condutora interna:
Daí:
Passo 4
(d) Como o sinal desse campo é positivo, então ele está direcionado para fora.
Passo 5
(e) A barra central induz uma carga na área mais interna da casca cilíndrica.
(f)Como a carga total da casca é , temos que na superfície mais externa da casca há uma carga de
Resposta
(a)
(c)
(e)
(f)