Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 23.7 - Ex. 28
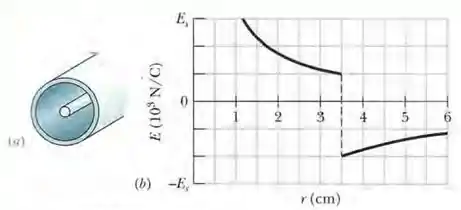
A Fig. 3-3 a mostra um cilindro fino, maciço, carregado, e uma casca cilíndrica coaxial, também carregada. Os dois objetos são feito de material não condutor e possuem uma densidade superficial de cargas uniforme na superfície externa. A Fig. 23-37b mostra a componente radial E do campo elétrico em função da distância radial r a partir do eixo comum. A escala do eixo vertical é definida por . Qual é a densidade linear de cargas da casca?
Passo 1
Olá, meu nobre amigo. Yuri aqui e estarei te ajudando nesta resolução. Aqui queremos descobrir a densidade linear da casca que cobre o cilindro fino.
Para isso, primeiro vamos observar o gráfico da figura (b).
Lembra-se da Lei de Gauss? Segundo ela, sendo a área superficial de uma superfície imaginária qualquer, e a carga interna a ela:
Assim, quando não há carga interna a essa superfície, o que acontece?
Acontece que !!!
Então, a gente já pode deduzir que, a coordenada a partir da qual o campo elétrico deixa de ser nulo é a aquela em que a superfície passa a ter um tamanho suficiente para abranger o cilindro interno carregado.
Passo 2
Sendo o raio desse cilindro, temos que:
Isolando :
Pelo gráfico, e . Então:
Passo 3
Agora, a gente vai aplicar a Lei de Gauss numa superfície externa aos dois cilindros
Assim:
Nesse caso, é dado pela soma das cargas de cada cilindro:
Olhando novamente para o gráfico, a gente pode perceber um ponto a partir do qual o comportamento do gráfico muda, passando a ser negativo. Esse ponto é o correspondente àquele em que a superfície “imaginária” da Lei de Gaus coincide com a do cilindro externo.
Aplicando essa Lei para uma superfície com raio igual ao raio do cilindro mais externo carregado ( , pelo gráfico) , temos:
Sendo .
Do passo anterior, a gente encontrou que , sendo e . Nesse caso, isolando , temos: