Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 16.Exercícios e Problemas - Ex. 10
Duas cascas esféricas condutoras concêntricas de raios e estão carregadas com cargas de sinais opostos e módulo , como se vê na figura 16.7. Calcule a energia associada ao campo elétrico gerado pelo sistema.
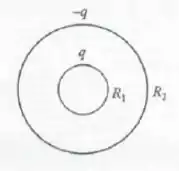
Passo 1
Eae galera! Belezinha? Seguinte, aqui nós vamos analisar as cascas como um capacitor esférico. Logo, temos, da fórmula padrão para capacitores esféricos:
Passo 2
Da fórmula da energia:
Logo,
Resposta
Resposta
Exercícios de Livros Relacionados
16.3E Calcule a energia eletrostática associada à interação entre dois prótons dentro de um núcleo, afastados 1,5 × 10 - 15m um do outro.
16.2E Calcule a energia potencial eletrostática de um átomo de hidrogênio, considerando o modelo semiclássico no qual o elétron percorre uma órbita circular de raio 0,051nm em torno do próton.
A posição de um corpo em movimento varia no tempo segundo a equação r = 80 + 15 t + 3 t 2 i - 5 t 2 j + 20 t k Onde as distancias são medidas em metros e o tempo é medido em segundos. Calcule (A) a ve
16.7E Calcule o raio clássico do próton, definido de forma análoga ao raio clássico do elétron.
Um elétron, partindo do repouso, é acelerado por um campo elétrico e se desloca para outro ponto onde o potencial elétrico é 1,0 ⋅ 10 4V mais alto. Qual é a velocidade adquirida pelo elétron?