Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 15.Exercícios e Problemas - Ex. 4

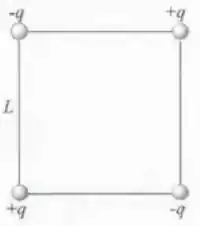
15.4E Calcule a força F sobre a esfera azul vista na Figura 15.13, supondo que as esferas têm diâmetro muito menor do que L .

Passo 1

Belezoca de motoca galerinha, nossa esfera azul possui outras 3 esferas que afetam a força elétrica resultante sobre ela.

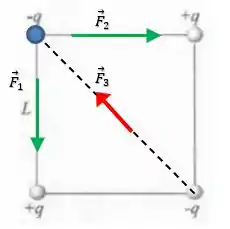
Podemos ver que para cargas opostas, a força elétrica F → 1 e F → 2 é atrativa, enquanto para cargas iguais a força F → 3 é repulsiva. Então se a gente montasse um diagrama de forças somente para a esfera azul, teremos:

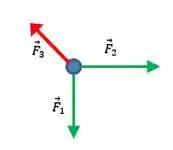
E na maciota, através do princípio da superposição das forças, teremos que a força resultante F → R vai ser dada por:

F → R = F → 1 + F → 2 + F → 3

Passo 2

Show de bolinhas, então bora lá encontrar cada uma dessas forças. Para calcular a força entre duas partículas, usamos a Lei de Coulomb dada por:

F E = k q 1 q 2 r 2

Onde q 1 e q 2 são as cargas das partículas em questão, r é a distância entre as cargas e k é nossa constante eletrostática. Dessa forma, para F → 1 , temos a interação entre as cargas + q e - q por uma distância dada por r = L , logo:

F → 1 = k + q - q L 2

F → 1 = k q 2 L 2

E como essa força F → 1 está no sentido negativo do eixo O y , isto é, de acordo com o vetor unitário - j ^ , podemos orientar essa força como:

F → 1 = k q 2 L 2 - j ^

F → 1 = - k q 2 L 2 j ^

Agora para a força F → 2 a interação também se dá entre as cargas + q e - q por uma distância L , tal que:

F → 2 = k q 2 L 2

A diferença aqui é que F → 2 está no sentido positivo do eixo O x , orientado pelo vetor unitário î , logo:

F → 2 = k q 2 L 2 î

Passo 3

Já para a força F → 3 , teremos uma interação repulsiva entre cargas - q e - q , e além disso a distância entre elas será dada pela diagonal do nosso quadrado:

d = L 2 + L 2

d = 2 L

Tal que o módulo da nossa força F → 3 é dada por:

F → 3 = k - q - q 2 L 2

F → 3 = k q ² 2 L 2

Mas além disso, a gente tem que orientar essa força exatamente na direção da reta que liga as duas cargas. E se a gente decompor essa linha de acordo com o ângulo θ :

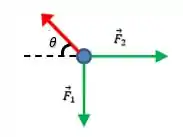
Teremos que a força decomposta é:

F → 3 = k q 2 2 L 2 - cos ⁡ θ î + sen ⁡ θ j ^

E como se trata de um quadrado perfeito, esse ângulo da diagonal divide 90 ° exatamente no meio, tal que θ = 45 ° :

F → 3 = k q 2 2 L 2 - cos ⁡ 45 î + sen ⁡ 45 j ^

F → 3 = k q 2 2 L 2 - 2 2 î + 2 2 j ^

F → 3 = k 2 q 2 4 L 2 - î + j ^

Passo 4

Portanto, pelo princípio da superposição das forças temos:

F → R = F → 1 + F → 2 + F → 3

F → R = - k q 2 L 2 j ^ + k q 2 L 2 î + k 2 q 2 4 L 2 - î + j ^

Reorganizando os termos:

F → R = - 4 k q 2 4 L 2 j ^ + 4 k q 2 4 L 2 î + k 2 q 2 4 L 2 - î + j ^

F → R = k 4 q 2 4 L 2 - k 2 q 2 4 L 2 î + k 2 q 2 4 L 2 - k 4 q 2 4 L 2 j ^

F → R = k 4 q 2 - 2 q 2 4 L 2 î + k 2 q 2 - 4 q 2 4 L 2 j ^

F → R = k q 2 L 2   4 - 2 4 î + k q 2 L 2   2 - 4 4 j ^

Portanto, trocando o sinal de j ^ , temos que:

F → R = 4 - 2 4 k q 2 L 2   î - j ^

Resposta

F → R = 4 - 2 4 k q 2 L 2   î - j ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

15.11E Um núcleo de ouro-197 tem 79 prótons e 118 nêutrons. Considerando esse núcleo com uma esfera de raio 6,4 × 10 - 15m uniformemente carregada com a carga de 79 prótons, calcule a intensidade do c
15.10E Calcule o valor total da carga negativa (de todos os elétrons) (A) na Terra e (B) na Lua, supondo que o número de prótons em cada um desses corpos seja igual ao número de nêutrons. (C) Suponha
15.8E As duas pequenas esferas metálicas vistas na Figura 15.16, de mesmo raio, estão suspensas por fios finos de náilon.Mostre que θ ' = θ . (B) Imagine que um fino fio condutor faça contato simultân
Uma casca esférica está carregada eletricamente de forma homogênea. Utilize a lei de Gauss e considerações de simetria para demonstrar que o campo elétrico no interior da casca é nulo.