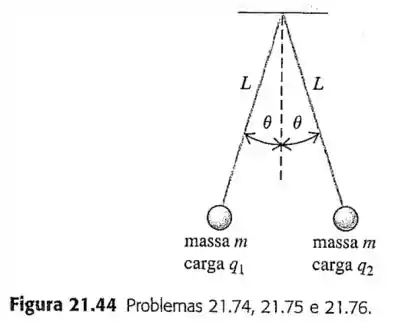
Duas esferas idênticas estão suspensas por fios de seda de comprimento , presos em um ponto comum (Figura ). Cada esfera possui . O raio de cada esfera é muito pequeno em comparação a distância entre as esferas, de modo que elas podem ser consideradas cargas puntiformes. Uma esfera possui uma carga e a outra possui uma carga diferente ; as esferas se afastam e, quando elas atingem o equilíbrio, cada fio forma uma ângulo com a vertical.
Faça um diagrama do corpo livre para cada esfera na posição de equilíbrio, identificado com símbolos todas as forças que atua sobre cada esfera.
Determine o módulo da força eletrostática que atua sobre cada esfera e calcule a tensão em cada fio
Com base nos dados do problema, o que você pode concluir sobre os módulos e os sinais das cargas e ? Explique sua resposta,
Agora um pequeno fio condutor é conectado entre as duas esferas, permitindo que ocorra uma transferência de cargas de uma para outra até que as duas esferas fiquem com cargas iguais; a seguir o fio é removido. Então, cada fio passa a formar um ângulo de com a vertical. Calcule os valores das cargas originais e . (Sugestão: a carga total sobre as duas esferas permanece constante.)
Passo 1
O diagrama de forças sabendo que a força elétrica é de repulsão será de:
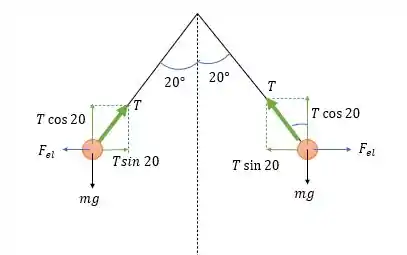
Sabendo que a massa é de então pela somatória das forças verticais em uma esfera a tração no cabo será de:
E pela somatória das forças horizontais em uma esfera a força elétrica calculada será de:
Em linhas gerais é como se fiséssemos
Passo 2
Como encontramos a força elétrica entre as esferas então a carga será de:

Onde e
E o que pode se afirmar entre essas duas cargas é que tem sinal oposto ao de , mas quanto cada uma vale individualmente nós não podemos afirmar com os dados que a questão nos fornece até o momento em que a letra nos é passada.
Passo 3
Já para a letra nos é afirmada que as duas cargas são iguais e que formam um ângulo de com a vertical, nessa situação a força elétrica será de:
E calculando essa força elétrica:
Onde e
Pois a sugestão era que a soma das duas cargas fosse igual entre esses dois estados.
Logo:
E
A relação entre as duas fórmulas é que:
Ou vice-versa