Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 22.Problemas - Ex. 57
Uma distribuição de cargas esfericamente simétricas, porém não uniformes, possui uma densidade dada por:
Em que é uma constante positiva. Mostre que a carga total contida na distribuição é igual a . Demonstre que o campo elétrico na região é idêntico ao campo elétrico produzido por uma carga puntiforme , situada em . Obtenha uma expressão para o campo elétrico na região . Faça um gráfico do módulo do campo elétrico em função da distância . Encontre o ponto para o qual o campo elétrico atinge seu valor máximo e calcule o valor desse campo elétrico máximo.
Passo 1
Como a densidade de carga volumétrica não é distribuída de forma uniforme, devemos utilizar um elemento diferencial de carga para, ao integrar, encontrar o valor total da carga em toda a região.
Consideremos, então, a região interior da distribuição.
Deixando a carga em função da densidade volumétrica de carga, ela terá a forma:
Considerando uma superfície gaussiana (em ) com o volume dado pela sua área de face e espessura :
Como a superfície é esférica:
Então, a carga total envolvida por essa superfície será:
Então:
Substituindo o valor da constante:
Logo:
Passo 2
Agora, para a região , consideramos uma superfície gaussiana com esse raio. Usando a lei de Gauss para ela, temos:
Como a superfície em questão é esférica:
Que é a equação do campo elétrico para uma carga puntiforme localizada no centro de uma esfera.
Passo 3
Da mesma forma, para a região , aplicamos a lei de Gauss para uma superfície gaussiana com esse raio. Logo:
No entanto, para essa região, a densidade de carga não é distribuída uniformemente.
Assim, devemos calcular a carga total envolvida pela superfície utilizando um elemento diferencial de carga em função dessa densidade, tal que:
Onde o volume desse elemento diferencial possui uma área esférica de raio , mas menor do que a superfície gaussiana, e uma espessura :
Assim, a carga total será dada pela integração dessa equação:
Então:
Substituindo o valor da constante:
Logo:
Portanto, como o campo elétrico é dado pela lei de Gauss:
Substituindo o valor da carga total envolvida:
Ou seja:
Passo 4
O gráfico do campo elétrico em função de pode ser dado por:
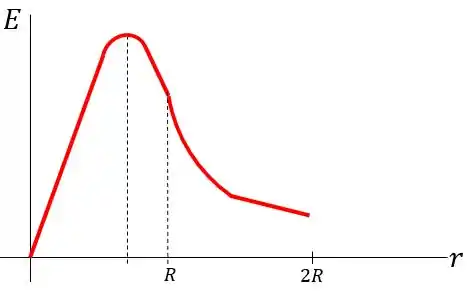
Passo 5
Para determinar o ponto máximo do campo elétrico, podemos utilizar um método de Cálculo , no qual derivamos a equação do campo e igualamos o resultado a zero para descobrir o valor de em que isso ocorre. Dessa forma:
Isolando a variável de interesse:
Portanto, o campo elétrico nesse ponto tem o valor:
Então: