Uma região do espaço contém uma carga positiva que está distribuída uniformemente ao longo de uma esfera de tal modo que a densidade volumétrica de carga é dada por:

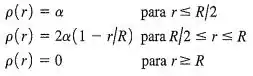
Nessas relações, é uma constante positiva com unidades de . Determine em função de e de . Aplicando a lei de Gauss, deduza uma expressão para o módulo do campo elétrico em função da distância . Faça esse cálculo separadamente para cada uma das três regiões. Expresse suas respostas em termos da carga total . Verifique cuidadosamente se seus resultados coincidem quanto às fronteiras entre as três regiões. Que fração da carga total está contida no interior da região ? Se um elétron com carga está oscilando em torno do ponto (o centro da distribuição) com amplitude menor do que , mostre que o movimento é harmônico simples. (Sugestão: Faça uma revisão da definição do movimento harmônico simples na Seção . Se, e somente se, a força resultante sobre o elétron for proporcional ao seu deslocamento do equilíbrio, então o movimento resultante será harmônico simples.) Qual é o período do movimento da parte ? Se a amplitude do movimento descrito na parte é maior do que , o movimento resultante é harmônico simples? Por quê?

Agora, para cada região, vamos verificar a carga total que é envolvida de acordo com a distância e determinar o campo elétrico da respectiva região a partir da lei de Gauss que é dada por:

Logo, para , a carga total envolvida é . Então:

Da mesma forma, a região envolve as cargas e :

Então:

Encontrando o MMC de todos os termos:

Nessa equação, simplificando todos os termos por , obtemos:

E, o resultado final para essa região pode ser dado por:

Ou seja:

Por último, para a região , a carga total envolveida é a soma das cargas nas três regiões. Então:

Mas como é zero, então só resta a soma dos outros dois termos:

Para calcularmos a quantidade da carga total que se encontra dentro da região , , vamos aproveitar os resultados obtidos no Passo , tal que essa quantidade é dada por:

Que representa aproximadamente:

Devemos lembrar, agora, que a força do movimento harmônico simples é diretamente proporcional a distância percorrida na oscilação e é dada por:

Assim, analisando a força gerada pelo campo elétrico da carga na região , temos:

Que possui a mesma forma da equação da força no MHS, onde:

Logo, o movimento nessa região é harmônico simples.

Usando o resultado que encontramos no Passo anterior, precisamos lembrar que o período do MHS é dado por:

Onde, nesse caso, é a massa do elétron. Então:

Para as regiões maiores que , temos que o campo elétrico não é mais diretamente proporcional ao deslocamento da oscilação , o que faria com que a força gerada pelo campo não tivesse mais a forma

E o movimento não seja mais harmônico simples.