Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 28.Problemas - Ex. 55
55- Duas espiras circulares idênticas, com de diâmetro cada uma, transportam uma corrente de no mesmo sentido. Essas espiras são paralelas entre si, e a distância entre elas é de . A linha é normal ao plano das espiras e passa pelos seus centros. Um próton é disparado a perpendicularmente a linha de um ponto médio entre os centros das espiras.
Determine o módulo, a direção e o sentido da força magnética que essas espiras exercem sobre o próton logo após ele ser disparado.
Passo 1
A fórmula para encontrar o campo magnético em um ponto fora do centro de espiras circular é de:
Então para uma partícula positiva abaixo:
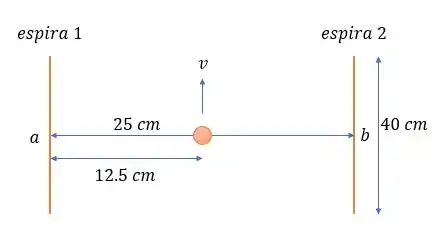
Como o ponto de interesse está a nas duas espiras nós temos uma intensidade de campo magnético para essa partícula igual a:
Passo 2
A força magnética no próton será de:
E o campo magnético sentido pela espira vai depender muito do sentido da corrente mas com certeza será apontando para a esquerda ou para a direita e como a velocidade está apontando para cima então a força magnética apontará para fora da folha ou para dentro da folha.