Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 17.4 - Ex. 34
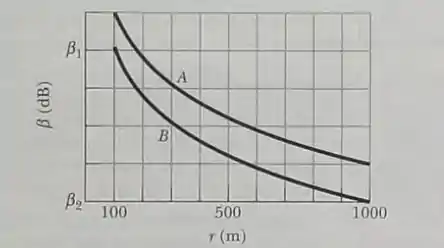
Duas fontes sonoras na atmosfera emitem isotrópicamente com potência constante. Os níveis sonoros das emissões estão plotados na Figura em função da distância das fontes.
A escala do eixo vertical é definida por e . Para , determine (a) a razão entre a maior e a menor potência e (b) a diferença entre os níveis sonoros das emissões.
Passo 1
(a)Belezoca galerinha, precisamos lembrar disso como um mantra: “olhar com atenção todos o enunciado e a figura, antes de partir pro ataque”.
Belezera, vamos então ver como fica essa brincadeira ai!
A primeira coisa que salta aos nossos olhos é que, no ponto do gráfico em que o nível sonoro da fonte é igual a
(em Já o nível sonoro da fonte é igual a:
Como surgiu esse resultado? O enunciado nos diz, com outras palavras, que a escala vertical desse gráfico é igual a:
Passo 2
Tá ok, mas como isso vai nos ajudar?
Aí é que está, meu caro jovem! Porque a malandragem é que agora podemos relacionar o nível sonoro com a intensidade da seguinte forma:
Mas calma lá meu patrão, saca só, vamos considerar que e são as potências das fontes (potências que são constantes, como diz o nosso enunciado). Elas relacionam-se com a intensidade da seguinte maneira;
Sendo e a intensidade da fonte e a distância até onde chega uma frente de onda propagada por ela.
A mesma coisa acontece com a fonte , tal que:
Passo 3
Beleza, a questão trabalha com níveis sonoros, mas voltamos a falar de intensidade. Qual a lógica disso?
Lembra como o nível sonoro e a intensidade se relacionam? É desse jeito:
Logo:
Como vimos no passo , a diferença entre os níveis sonoros no ponto em que vale . Vamos usar isso na expressão acima, considerando as intensidades das fontes e e ver onde chegaremos!
Tal que:
E agora vamos usar aqui as expressões do Passo 2! Saca só:
Passo 4
Finalmente, lembrando que a subtração de dois logaritmos é igual ao logaritmo da divisão:
A gente consegue transformar a última equação do passo 3 no seguinte:
Daí, a gente chega na nossa procurada resposta:
Logo:
