Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.1 - Ex. 25
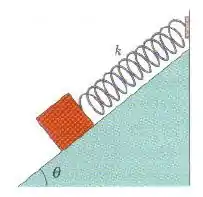
Na figura, um bloco pesando , que pode deslizar sem atrito em um plano inclinado de ângulo , está ligado ao alto do plano inclinado por uma mola de massa desprezível de de comprimento quando relaxada e cuja constante elástica é . (a) A que distância do alto do plano inclinado fica o ponto de equilíbrio do bloco? (b) Se o bloco é puxado ligeiramente para baixo ao longo do plano inclinado e depois liberado, qual é o período das oscilações resultantes?
Passo 1
Show de bolinhas pessoal, o ponto de equilíbrio do bloco é o ponto onde todas as forças se cancelam. Vamos pensar nas forças que atuam sobre o bloco. (Definindo o sentido positivo como sendo o sentido da descida do plano).
Empurrando o bloco plano abaixo temos uma componente da força peso cuja fórmula nós conhecemos muito bem:
E puxando o bloco plano acima temos a força elástica da mola, que segue a lei de Hooke:
As forças perpendiculares ao plano (a normal e a outra componente do peso) se cancelam, já que o bloco só se move na direção da superfície do plano.
Passo 2
Iradoso, pela segunda lei de Newton, temos que:
No ponto de equilíbrio, , de forma que obtemos:
E por isso a distorção da mola no ponto de equilíbrio vai ser:
E somando isso ao tamanho da mola, obtemos a distância até o topo do plano, dada por:
Passo 3
Belezoca, agora na letra (b), temos que essa questão é uma espécie de pegadinha.
Eles só querem que a gente encontre o período da oscilação da mola da figura. Que segue essa fórmula bem conhecida:
Você poderia pensar que temos que fazer alguma coisa mirabolante para considerar o efeito da gravidade e tal, mas não precisa. Essas fórmulas aí continuam válidas, seja na horizontal, no plano inclinado ou de cabeça pra baixo ou na superfície da lua. Sendo assim:
Resposta
(a)
(b)