Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 35.1 - Ex. 13

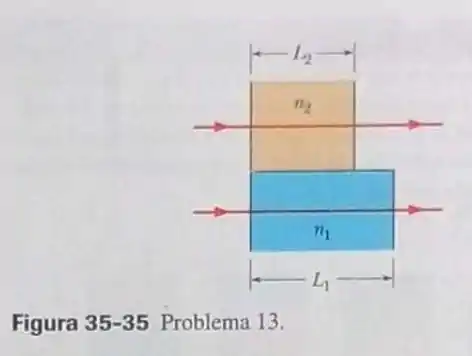
Duas ondas luminoas no ar, de comprimento de onda 600,0 nm, estão inicialmente em fase. AS ondas passam por camadas de plástico, como na Fig. 35-35, com L 1 = 4,00 μ m , L 2 = 3,50 μ m , n 1 = 1,40 e n 2 = 1,60 , (a) Qual é a diferença de fase, em comprimentos de onda, quando as ondas saem dos dois blocos? (b) Se as ondas são superpostas em uma tela, com as mesma amplitude, a interferência é construtiva, destrutiva, mais próxima de construtiva ou mais próxima de destrutiva?

Passo 1

  1. Escolhemos um eixo x horizontal com a origem na borda esquerda dos blocos de plástico. Entre x = 0 e x = L 2 , a diferença de fase é dada pela Eq. 35-11 com L substituído por L 2 . Entre x = L 2 e x = L 1 , a diferença de fase é dada pela Eq. 35-11 com L substituído por L 1 - L 2 e n 2   substituído por 1, já que o raio de cima da Fig. 3535 passou a se propagar no ar, cujo índice de refração é aproximadamente igual a 1. Combinando essas diferenças e fazendo λ = 0,600   μ m , temos:

    2. L 2 λ n 2 - n 1 + L 1 - L 2 λ 1 - n 1 = 3,50 μ m 0,600 μ m 1,60 - 1,40 + 4,00 μ m - 3,50 μ m 0,600 μ m 1 - 1,40 = 0,833

    Passo 2

  2. Como a resposta do item (a) está mais próxima de um número inteiro do que de metade de um número ímpar, a interferência é mais próxima de construtiva do que de destrutiva.

Resposta

  1. 0,833
  2. mais próxima de construtiva do que de destrutiva
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que o comprimenro de onda no ar das duas ondas da Fig. 35-4 seja λ = 500n m . Determine o múltiplo de λ que expressa a diferença de fase entre as ondas depois de atravessar os dois materiais (
A velocidade da luz amarela (produzida por uma lâmpada de sódio) em um certo líquido é 1,92 ⋅ 10 8m / s . Qual é o índice de refração para essa luz?
2 - Fantasma da TV. O chamado fantasma da TV é uma imagem que se forma sobre a tela em virtude da superposição das ondas eletromagnéticas que chegam diretamente sobre a antena e das ondas que chegam i
1 - (a) Sabendo que a distância entre a Terra e a Lua é de 384000k m , quanto tempo leva a luz para viajar da Lua até a Terra? (b) A luz emitida pela estrela Sirius leva 8,61 anos para chegar até a Te
4 - Radiação ultravioleta. Há duas categorias de raio ultravioleta. O ultravioleta A (UVA) possui um comprimento de onda que varia de 320n m a 400n m . Ele não é tão prejudicial à pele e é necessário