Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 22.Problemas Adicionais - Ex. 65

Duas partículas , ambas com uma carga de valor absoluto 12 nC, ocupam dois vértices de um triângulo equilátero com 2,0 m de lado. Determine o módulo do campo elétrico no terceiro vértice (a) se as duas cargas forem positivas e (b) se uma das cargas for positiva e a outra for negativa.

Passo 1

Temos o seguinte problema, duas cargas de módulo Q = 12nC colocadas nos vértices de um triângulo equilátero com d=2,0 m de lado. Para compreender, fica muito mais fácil com uma figura, vamos primeiro olhar para o caso (a), onde as cargas são positivas.

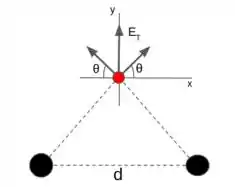
Temos que as componentes horizontais se anulam sobrando apenas as componentes verticais. Agora podemos utilizar a formula do campo elétrico.

Passo 2

Relembrando a formula do campo elétrico:

E = Q 4 π ε 0 d 2

Porem, como estamos falando da componente y do campo elétrico, temos que multiplicar o campo E por sin(θ), já que queremos o cateto oposto ao ângulo:

E y = E s i n θ

Bem, esse é o campo de uma das cargas. Dessa forma:

E T = E y + E y = 2 E s i n θ

Lembrando que no caso de triângulos equilátero, o ângulo interno é 60º, temos:

E T = 2 Q 4 π ε 0 d 2 s i n θ

E T = 2 12 x 10 - 9 4 π 8,85 x 10 - 12 2,0 2 s i n 60 º = 46,7 N / C

Passo 3

No caso (b) onde as partículas tem sinais opostos, o campo elétrico tem componente apenas na direção horizontal, pois as componentes verticais se anulam. Temos o mesmo caso, porém, como queremos agora os catetos adjacentes multiplicamos o campo elétrico pelo cos(θ):

E T = E x + E x = 2 E c o s θ

E T = 2 Q 4 π ε 0 d 2 c o s θ

E T = 2 12 x 10 - 9 4 π 8,85 x 10 - 12 2,0 2 c o s 60 º = 27 N / C

Resposta

(a) E T = 46,7 N / C

(b) E T = 27 N / C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fio plástico retilíneo e não condutor de 8,5c m de comprimento carrega uma densidade de carga de + 175n C / m , distribuída uniformemente ao longo do comprimento. Eles está sobre a superfície horiz
Considere o dipolo elétrico do Exemplo 21.15(a) Deduza uma expressão para o módulo do campo elétrico produzido pelo dipolo em um ponto sobre o eixo x da figura 21.34. Qual é a direção e o sentido dess
Três cargas se situam nos vértices de um triângulo isósceles, como indica a figura 21.43. As cargas de ± 5μ C formam um dipolo.(a) Determine a força (módulo, direção e sentido) que a carga - 10μ C exe
Uma carga de - 6,5n C está uniformemente distribuída sobre a superfície da face de um disco não condutor de raio 1,25c m .(a) Determine o módulo, a direção e o sentido do campo elétrico que esse disco
Duas partículas puntiformes que têm cargas + 4 q e - 3 q estão separadas por uma distância d . Use linhas de campo para desenhar uma visualização do campo elétrico na vizinhança do sistema.Desenhe as