Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 21.4 - Ex. 21
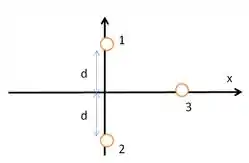
Na Fig. 21-31, as partículas e , de carga , estão no eixo , a uma distância da origem. A partícula , de carga , é deslocada ao longo do eixo , de até . Para que valor de o módulo
da força eletrostática exercida pelas partículas e sobre a partícula é (a) mínimo e (b) máximo? Qual é o valor (c) mínimo e (d) máximo do módulo?
Passo 1
E aí! como vai? 😊
Nesse problema temos um sistema com três partículas carregadas, onde e . e estão sob o eixo a uma distancia da origem cada uma e se desloca de a .
A partir daí, nosso objetivo é obter o ponto onde a força eletrostática sofrida por seja mínima e máxima e tambem queremos saber qual é o modulo das forças nesses pontos.
Parece complicado? 🤔
Para solucionar esse problema, temos que lembrar da lei de Coulomb
Onde é a constante eletrostática, e são as cargas e a distania entre elas.
Veja só! 👀
Passo 2
Uma opção para analisar os valores máximos e mínimos da força eletrostática a qual está submetida, é fazer o gráfico da força eletrostática equacionada abaixo, em função da distância :
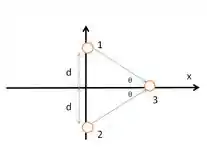
Plotando esse gráfico, encontramos:
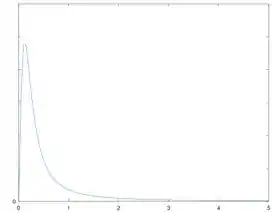
Observando os limites do gráfico, podemos perceber que a força é mínima quando e é máxima quando , aproximadamente
Tranquilo até aqui? 😁
Passo 3
(c) A força resultante em é nula.
(d) A força máxima em é igual a aproximadamente . Só substituir na nossa função:
E aí! entendeu tudo? Responde Aí!😬
