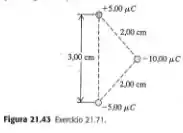
Três cargas se situam nos vértices de um triângulo isósceles, como indica a figura 21.43. As cargas de formam um dipolo.
(a) Determine a força (módulo, direção e sentido) que a carga exerce sobre o dipolo.
(b) Para um eixo perpendicular à linha que liga as cargas de no meio dessa linha, ache o torque (módulo, direção e sentido) exercido sobre o dipolo pela carga .
Passo 1
(a) Beleza, antes de fazer as contas, vamos ver como está essa força no dipolo: pelo princípio da superposição, a força que a carga exerce sobre o dipolo será a soma das forças que ela exerce sobre cada carga do dipolo:
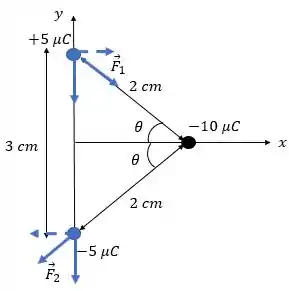
Como as cargas do dipolo estão a uma mesma distância da outra carga e elas possuem um mesmo valor em módulo, as componentes em das duas forças se cancelam (elas estão em pontilhado ali). E, então, a força resultante sobre o dipolo será a soma das componentes verticais das duas forças:
Só que, pela imagem, podemos ver que:
E:
Passo 2
Vamos calcular primeiro, passando :
Substituindo :
Repare que a força elétrica depende apenas dos módulos das cargas e da distância entre elas. Então, como as cargas do dipolo são iguais em módulo e estão a uma mesma distância da , . E:
E:
Ou seja, também vamos ter que . E, consequentemente, . O sinal negativo ocorre pelas forças estarem no sentido negativo de .
Falta só o seno! Olhando para a imagem, temos:
Substituindo na :
Onde está na direção da carga positiva do dipolo para a carga negativa.
Passo 3
(b) Vamos olhar para a imagem de novo:
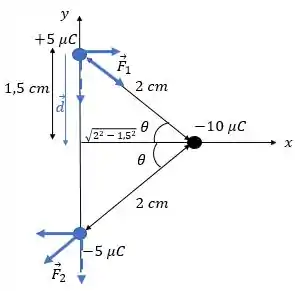
Vamos usar a origem como o eixo de rotação, ok? Dessa forma, as componentes verticais das forças não vão exercer torque, já que o ângulo entre elas e a distância que une as cargas ao eixo de rotação é e, como , o seno de zero vai anular todo o torque.
Assim, apenas as componentes horizontais exercem torque. Então, a força resultante que exerce torque será a soma das duas, como elas são iguais em módulo (pelas cargas estarem a mesma distância da terceira carga e terem valores iguais em módulo), a força resultante será:
E podemos calcular essa componente assim:
Onde e já calculamos :
Com isso:
Passo 4
Agora, falta só calcular o torque exercido por essa força em relação ao eixo que colocamos na origem:
Substituindo os valores que temos, onde :
Esse torque gira o dipolo no sentido horário (só colocar os dedos na direção de alguma componente horizontal e o sentido do torque é para onde você fecha os dedos).
Resposta
(a). Onde está na direção da carga positiva do dipolo para a carga negativa.
(b), no sentido horário.