Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 23.Exercício - Ex. 39
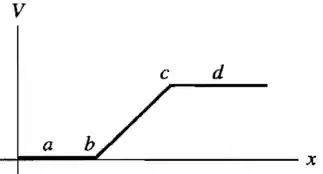
Duas placas metálicas paralelas grandes possuem densidade de cargas com mesmo módulo, mas sinais contrários (figura abaixo). Suponha que elas estejam próximas o suficiente para serem tratadas como placas infinitas ideais. Considerando zero o potencial na superfície esquerda da placa negativa, faça um gráfico do potencial em função de x. Inclua todas as regiões da esquerda das placas até a direita das placas.
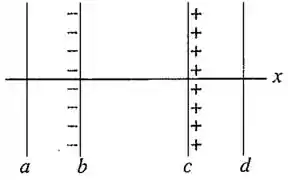
Passo 1
Fora das placas o campo elétrico é nulo. Como:
Fora das placas o potencial é constante.
Então de e
Passo 2
Já dentro da placa temos um campo elétrico uniforme que tem direção do + para o -. Ou seja, ele sai da carga positiva e vai para a placa negativa.
Além disso, podemos usar a relação:
Como E é uniforme dentro da placa, V vai variar linearmente com a distância. Quanto maior a distância, maior será o V. Então, V cresce linearmente da esquerda para a direita.
Passo 3
Montando o gráfico com as informações:
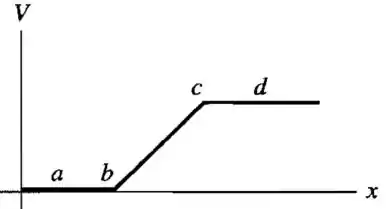
Resposta
