Duas placas paralelas muito grandes estão separadas por uma distância igual a . A placa A possui uma densidade superficial de carga uniforme igual a, e a

placa B, que está à direita da A, possui uma densidade superficial de carga uniforme igual a ,. Suponha que as placas sejam suficientemente grandes para que possamos considerá-las infinitas. Calcule o módulo, a direção e o sentido do campo elétrico resultante que essas placas produzem em um ponto

(a) 4,00 cm à direita da placa A;

(b) 4,00 cm à esquerda da placa A;

(c) 4,00 cm à direita da placa B.

Olá, tudo bem? Vou ajudar você aqui!

Antes de mais nada, precisamos lembrar que o campo elétrico de uma placa infinita é:

Então o campo em cada ponto vai ser dado a partir da orientação dos campos. Vou primeiro calcular o módulo de cada um:

Agora vou fazer um desenho de como fica o campo. O campo elétrico numa placa negativa é para dentro, então nessa situação temos:

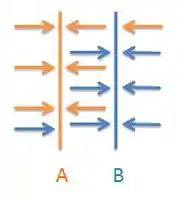
Letra (a):

Entre as placas, o campo de é negativo e o de é positivo. Os valores nós calculamos ali em cima, então é só substituir: